近期疫情逐漸升溫, 每日新增的確診數都在百人以上。
在 5/23 日, 指揮中心提出了「校正回歸」, 意即將因檢驗過程延宕的時間才確認陽性的確診數, 反推至其檢驗日。
採取校正回歸的理由是此舉比較能還原確診數增加的趨勢, 減少不必要的恐慌。
但此舉受到多人批評, 疑似有掩蓋確診數大量增加的行為, 因此每日新增確診數應該加上校正回歸數, 方能反應實際情況。
本文將以統計學的角度, 討論何種方式(考慮校正回歸與不考慮校正回歸)的趨勢是比較接近真實的情況。

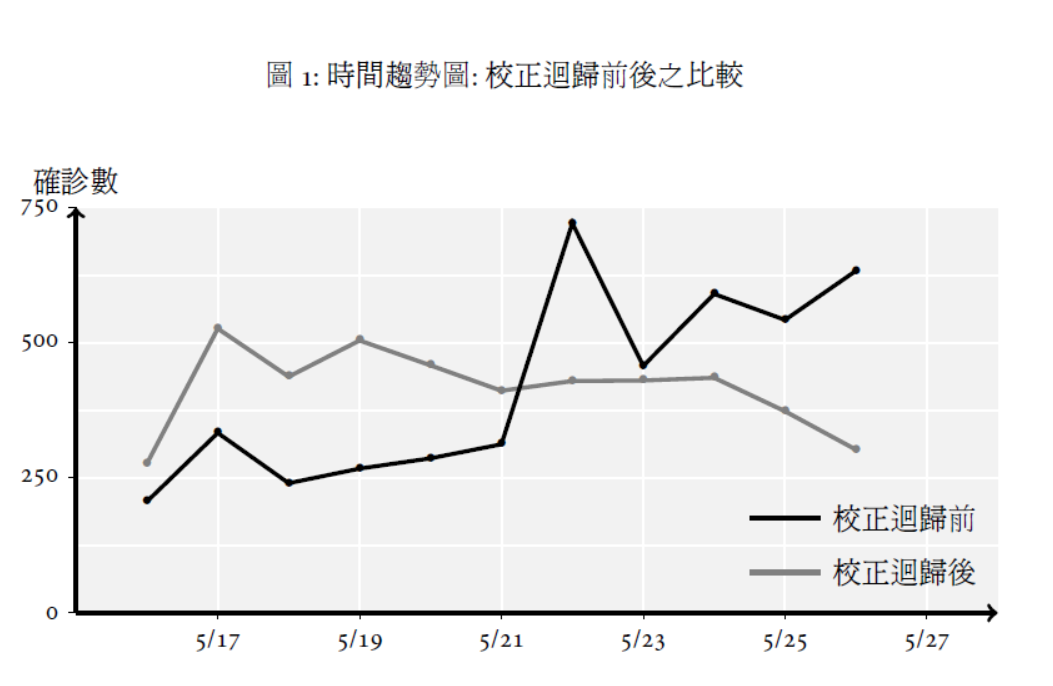
表1是校正迴歸前後的資料, 圖1 則畫出了時間趨勢圖, 時間則由 5/16 至 5/26 日。
可以看出, 若不考慮校正迴歸, 則看起來確診數有上升的趨勢; 若考慮校正迴歸, 則確診數看起來有緩和甚至下降的情況。
那我們應該相信哪一個呢? 或者是哪一個才能反應真實的趨勢?

在此, 我使用了兩個常用的時間趨勢模型, 線性趨勢模型與二次式趨勢模型, 嘗試預測 5/27 日之確診數。
考慮校正回歸的模型中, 被預測變數是每日新增確診數; 在不考慮校正迴歸的模型中, 被預測變數是每日新增確診數加上校正回歸數。
在此設定 5/16 日之t=1, 因此 5/26 日之t=11, 以此類推。回歸模型估計結果如下:

※考慮校正迴歸

1.線性趨勢模型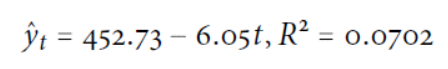


2.二次式趨勢模型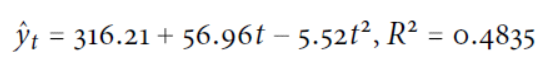

※不考慮校正迴歸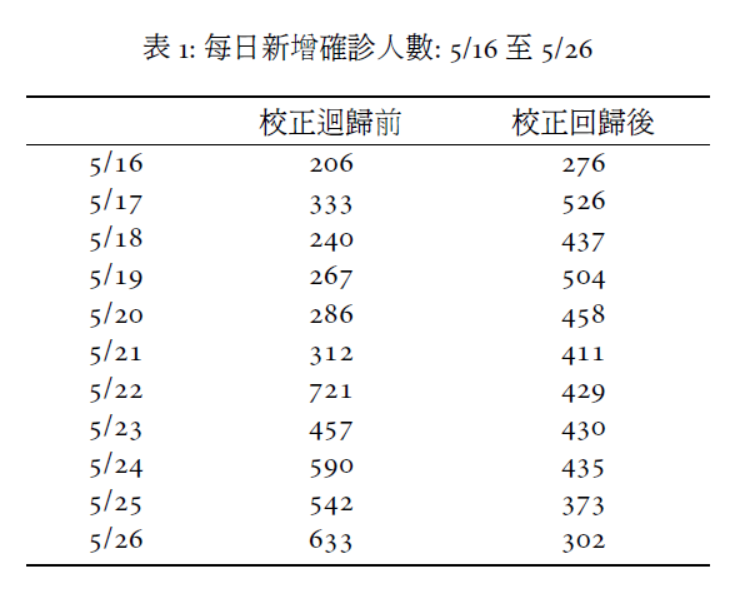

1.線性趨勢模型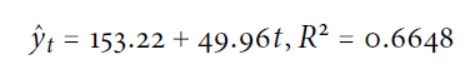

2.二次式趨勢模型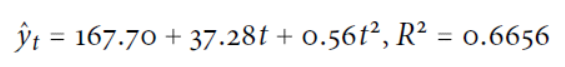

在小樣本的情況下, 判定係數僅供參考即可, 我們將重點放在預測的準確性, 意即 5/27 日的預測值與實際值的差距。
5/27 對應的 t=12, 代入模型中即可得到預測分別為

◆ 線性趨勢: 380(新增本土確診), 681(新增本土確診+校正回歸數)
◆ 二次趨勢: 244(新增本土確診), 695(新增本土確診+校正回歸數)

而實際上, 5/27 的新增確診數為 401 人, 新增本土確診+校正回歸數為 667 人。
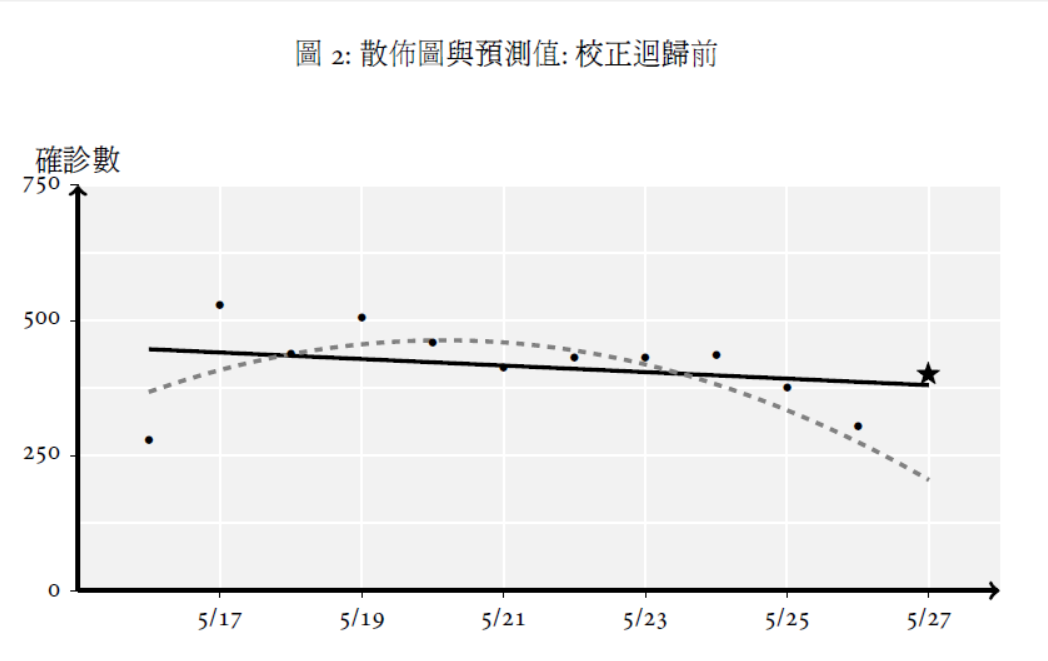
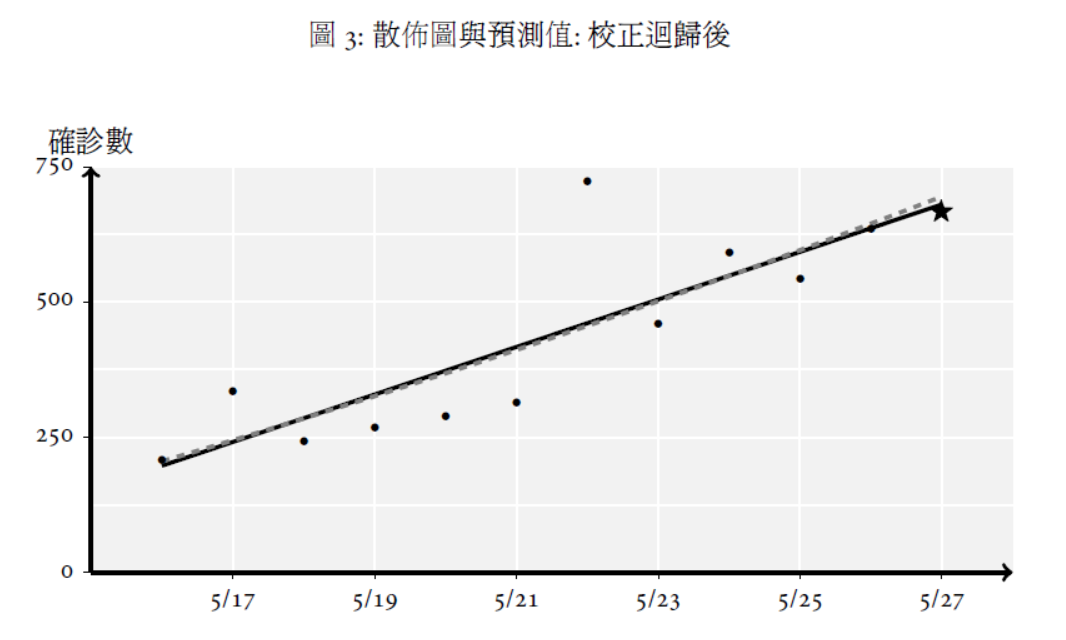
預測的圖示請參見2 與3, 可以看出線性趨勢對於校正前後的預測相當準確, 可以暫時相信兩種作法都是可以說服人的。

特別注意到, 評估預測的表現不能只看一期的結果, 應該要多進行幾期的預測再比較其平均表現, 因此有興趣的讀者, 可以根據每日更新的資料持續的進行預測。
對於統計軟體 R 語言對於本議題的程式有興趣的讀者, 可以參閱。