中央極限定理 (central li mi t th eorem) 的最廣泛的應用為給定一組隨機樣本

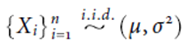
其中意即隨機變數的期望值與變異數需存在。 給定 n 足夠大時 (sufci entlylarge),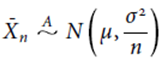

意即只要樣本數夠大, 樣本平均的抽樣分配將”看起來”像常態分配。 但不是任意分配與任意樣本數均適用中央極限定理。 舉例來說,

1. 若資料母體為均勻, 則因為均勻分配是對稱分配, 因此不需太多樣本數, 就能使得樣本
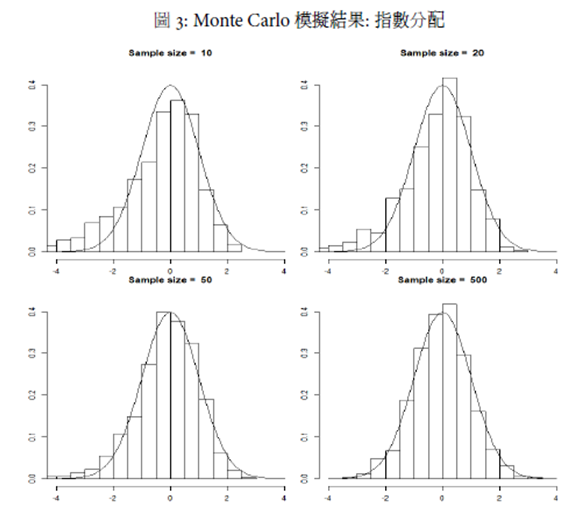
   平均近似於常態分配。
   
2. 若資料母體為指數分配, 則因為指數分配是右偏分配, 則需要更多樣本數, 才能使得樣本平均近似於常態分配。
   
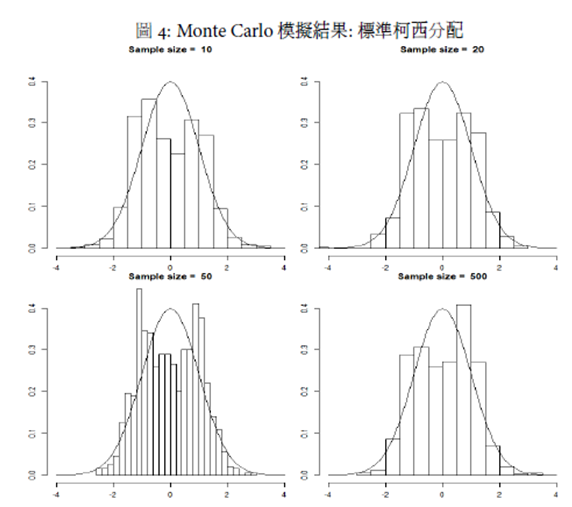
3. 若資料母體為標準柯西分配, 則因為其分配的期望值與變異數均不存在, 因此無論樣本數有多大, 樣本平均都不會近似於常態分配。

而我們可以利用 R語言, 透過 Monte Carlo 模擬驗證以上的論述。 為了方便與常態分配作比較, 我們將樣本平均標準化, 並與標準常態分配的密度進行比較。

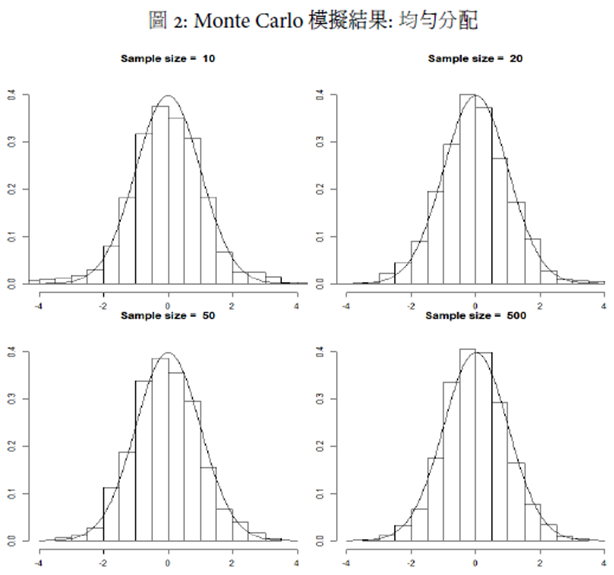
R語言的程式碼請參見圖:1 模擬結果如圖 1 所示。 可以發現, 均勻分配在小樣本時, 樣本平均之分配即與標準常態分配很類似。 而指數分配在小樣本時, 樣本平均仍然保持著右偏分配的特性。 標準柯西分配則無論樣本數, 其分配型態均與標準常態分配相去甚遠。 這些結果與原本的預期一致。

*作者為臺灣大學經濟學博士, 其研究領域為應用時間序列分析 (applied time series econometrics)。 對於本文有任何指教或者建議, 請來信至 ksherryhsu@hotmail.com, 或至 Facebook 搜尋 "許誠哲"。

有三種分配, 運行時將第 9 至 11 行, 根據欲選分配的程式碼對應之行的行首的 # 字號取消後再運行。