在統計學中, 令 表示為某隨機試驗的所有可能結果, 並假設每一個出象的出現的機率皆相同。事件 A 發生的古典機率定義為

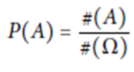
集合元素的個數之總和。對於, 大多仰賴窮舉或者利用排列組合計算。舉例來說, 定義隨機試驗為投擲一公正骰子, 令A為投擲出偶數的事件, 則

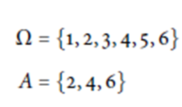
因此, 故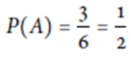意即有 1/2 的機率投擲出偶數。

但若的計算上較為複雜, 則不容易驗證其計算過程是否出錯, 此時可以透過 Monte Carlo 模擬來作為驗證。舉例來說, 在夜市中有一種6x6的賓果遊戲, 其圖示請參見圖1。

遊戲方法為在 36 張牌中, 任意選擇 15 張牌後, 若可以連成線即可換到獎品。可以連成的線有橫或豎各 6 條線與 2 條對角線, 共 14 種。其遊戲結果可能連成 1 連線、2 連線或者 3 連線。

以下我們開始計算各連線數出現的機率:

• 樣本空間的可能組合數為
  
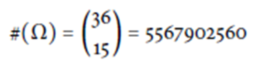
• 3 連線需要共用 3 張牌, 因此先選對角線 (2 種可能), 之後再選直線 (6 種可能), 最後一條橫線則只剩 5 種可能, 因此
  
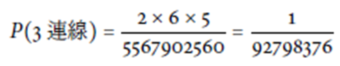
  這個機率是威力彩頭獎中獎機率的 1/4, 基本上不會出現。
• 2 連線中, 需選擇其 2 連線的類型。
  ﹣若是直線配橫線 (36 種組合)、直線配對角線 (12 種組合)、橫線配對角線 (12 種組合),此時會有一張牌同時在這兩條線中, 剩下 4 張牌則任意選擇。
  ﹣若是雙直線 (15 種組合)、雙橫線 (15 種組合)與雙對角線 (1 種組合), 則剩下 3 張牌任意選擇。     此外, 不要忘記 2 連線的組合中包含了 3 連線, 因此要扣掉, 故所求為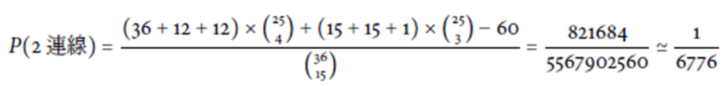
• 1 連線中則較簡單, 只要從 14 條線中選擇 1 條, 剩下 9 張牌任意選擇, 最後再扣掉 2 連線與 3 連線的情況即可。 故所求為
  

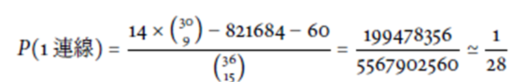
可以看出, 古典機率的計算相當複雜, 若有考慮不周詳的地方, 此時即會出錯, 因此不容易進行驗算。此時可以利用電腦進行 Monte Carlo 模擬, 如果重覆模擬數夠多, 此時電腦模擬出的結果的樣本比例將會與古典機率的結果相當接近。在此我們考慮 1 億次模擬, 程式碼請參見圖2。
以期望次數來說,

• 1連線的期望次數為
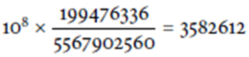
• 2連線的期望次數為

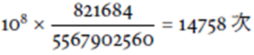
在這 1 億次模擬中, 出現了 3569708 次 1 連線, 14613 次 2 連線, 3 連線則沒有發生過。可以發現模擬的樣本比例與古典機率的差距都在萬分之 1 左右, 這個差距會隨著重覆模擬數增加而減少。但是, 寫出程式碼相較於計算古典機率則簡單許多。因此遇到計算古典機率中, 計算上比較複雜的時候, 可考慮使用Monte Carlo 模擬估算大概的機率或者作為驗算。

最後, 我們留給讀者一個小小的作業。 在知名的撲克牌遊戲 10 點半中, J、Q、K 都視作半點。請利用 Monte Carlo 模擬估算出現「過五關」的機率, 意即前 5 張牌的點數和小於 10 點半的機率。