研究所考試
在上一篇我們介紹了紅黑樹的刪除步驟,我們用了「先處理結構、再維持紅黑樹性質」這句話作為總結。首先使用二元搜尋樹的刪除規則,將要被刪節點轉換為刪除至多只有一個子節點的情況,並且以後繼節點取代該節點。接下來會依照實際被刪除的節點顏色,來決定是否需要進行額外調整,若實際被刪除節點的顏色為黑色,則需要進行刪除修正的步驟(delete_fixup)。修正過程透過檢視兄弟節點與其子節點的顏色,搭配顏色變換與旋轉操作,逐步消除黑高有問題的情況,直到紅黑樹的所有性質重新成立。
在本次的文章裡,我們會介紹紅黑樹與2-3-4樹的關係,讓各位讀者明白紅色黑色節點與2-3-4樹中2-節點、3-節點與4-節點的關聯性。其中紅黑樹每一條路徑上黑色節點數量相同的原則,就是因為2-3-4樹的所有葉節點需要在同樣的高度。筆者也特別挑選了在歷屆試題當中比較特別的題型,希望各位讀者能在閱讀完後徹底攻略紅黑樹!
我們在之前的文章裡有稍微提及,紅黑樹是2-3-4樹的二元搜尋樹版本。2-3-4樹是B-tree的一種,數字的2-3-4代表每個節點可以是2-節點、3-節點或是4-節點,數字對應的是該節點有多少個子節點。作為B-tree的一員,紅黑樹需要遵守一項重要原則:「所有葉節點位於同一層」,以此維持高度在O(logn)這個等級。下圖為2-3-4樹的示意圖,其中只有一個key值的節點為2-節點(例如根節點),而左下包含兩個key值(1,2)的節點為3-節點,右下包含三個key值(10,11,12)的節點為4-節點。
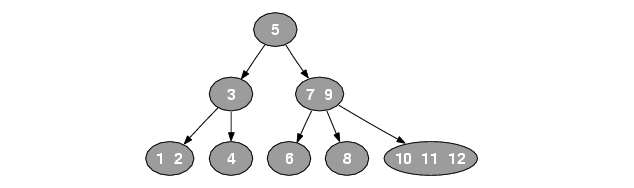
在簡單介紹完2-3-4樹後,我們就要來說明它與紅黑樹的關係了。紅黑樹裡面的「紅色」與「黑色」節點,其實就是在模擬2-3-4樹當中的節點結構。每一個紅黑樹的黑色節點,如果它的左右子節點是紅色的,就代表它們在2-3-4樹當中是屬於同一個節點。例如剛才提到的4-節點(10,11,12),轉換成紅黑樹時,11就會是黑色節點,而10與12節點會是紅色節點,分別成為11的左右子節點。換句話說,不管是2-節點、3-節點或是4-節點,在轉換成紅黑樹時都會轉出一個黑色節點,其餘的key值則會轉為紅色節點。這也是為什麼紅黑樹的規則裡有一項是「每個節點到它底下的每一個外部節點的路徑,經過的黑色節點數量相同」,因為2-3-4樹的特性確保所有葉節點位於同一層,因此每一條路徑經過的節點數量相同,也就代表在紅黑樹中經過的黑色節點數量相同。
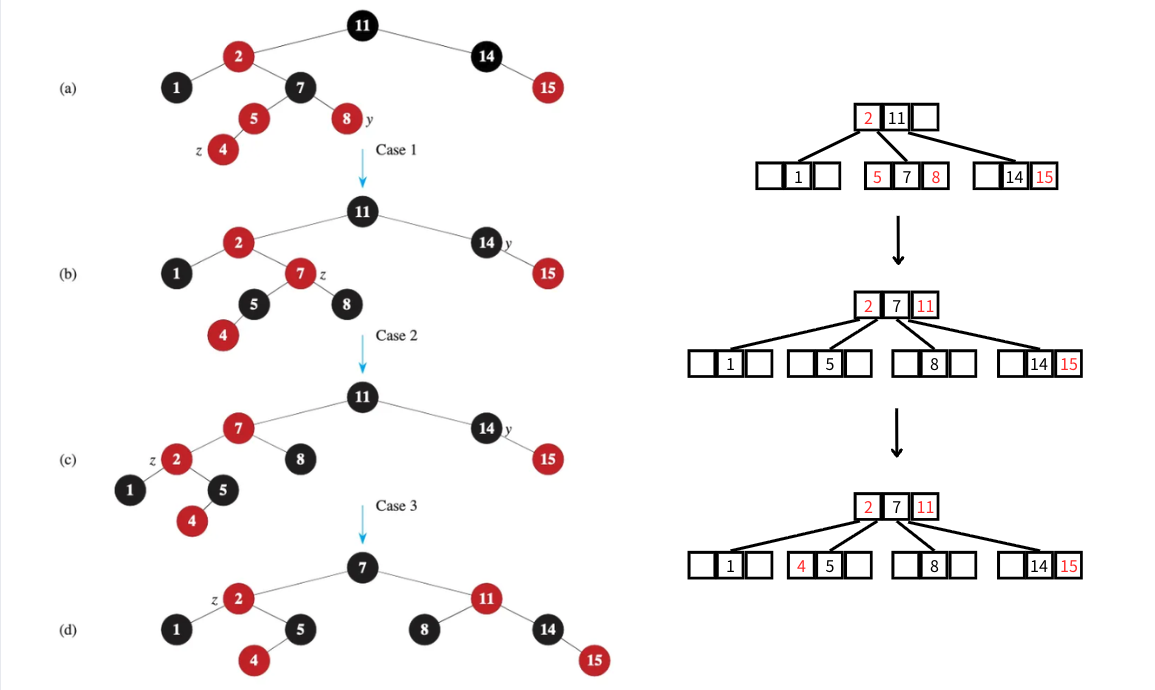
這時候讀者可能會想問:「知道紅黑樹與2-3-4樹的關係,有什麼用呢?」對於考試來說,最大的用處就是「驗算」!既然兩者之間是相同概念不同呈現方式,當然就可以互通啦!我們在介紹紅黑樹插入時,使用的範例在一次插入就遇到了四種狀況的其中三種,其中只要任何一個過程出錯,就會讓最後的結果出現問題。這時候我們如果把原來的紅黑樹先轉換成2-3-4樹,一樣進行插入,再將最後的結果還原回紅黑樹,就能協助確認有沒有失誤了!
至於要如何轉換呢?首先,按照定義,把黑色節點跟子節點當中的紅色節點進行合併,例如11的子節點當中,2是紅色,因此在2-3-4樹當中,11跟2就屬於同一個節點。轉換完成後,就按照2-3-4樹的插入步驟來插入4這個key值。2-3-4樹的插入步驟很簡單,在插入的過程裡遇到的4-節點,轉換為2-節點即可(split)。例如在插入過程裡,包含5,7,8這三個key值的節點為4-節點,因此需要進行split操作,將中間的key值交給上面的節點,而剩下的key值分裂為左右兩個節點,形成兩個2-節點。再來,將要插入的key值4放到對應位置後,2-3-4樹的插入便處理完成了。最後,只需要用相同的技巧,將2-3-4樹還原回紅黑樹,就可以得到與直接用紅黑樹操作相同的結果啦!
- 歷屆試題
-
紅黑樹在資工所是相當常出現的考題,而插入的操作又是最頻繁出現的題型,例如成大資工在113年的第8題就是相當典型的插入操作考法,讀者們別忘了可以用2-3-4樹驗算喔!而這裡我們要來討論的是比較特別的考法,出現在台大資工111年的考卷當中:
- (5 points) Consider a red-black tree with 𝑛 internal nodes, where 𝑛 is even. At most how many of them can be a black node with one red child?
- (A) 𝑛/2
- (B) 𝑛
- (C) ⌊log2(𝑛+1)⌋−1
- (D) ⌊log2(𝑛+1)⌋
- (E) none of the other choices
- (5 points) In the red-black tree with 26 nodes that reaches the solution of the problem above, what is the maximum height of the tree? A tree with one node is assumed to have height 1.
- (A) 5
- (B) 6
- (C) 7
- (D) 8
- (E) 9
首先第14題問的是,一棵紅黑樹有 𝑛 個內部節點,並且 𝑛 是偶數,此時最多能有多少個黑色節點是恰好有一個紅色子節點呢?首先觀察題目的主角,也就是「恰好有一個紅色子節點的黑色節點」,既然題目要求「最多」,我們當然希望這樣的結構越多越好。我們可以把整棵樹想成2-3-4樹,題目的主角就會變成3-節點(一個黑色節點配一個紅色子節點),而這樣的3-節點可以作為基本單位來充滿整棵2-3-4樹,也就是說,一整棵2-3-4樹的所有節點都是3-節點,並不會違反任何2-3-4樹的規則。由此推論可得,如果原本的紅黑樹有 𝑛 個節點,其中有一半是黑色節點、一半是紅色節點,它們便可以兩兩搭配成為一組,成為一個在2-3-4樹中的3-節點,而這樣的個數是 𝑛/2,也就是第14的正確答案。
再來,第15題接著問,如果符合上一題條件的紅黑樹總共有26個節點,那這棵樹的最大樹高是多少(假設單一節點高度是1)?如果只知道紅黑樹的特性,也就是「每個節點到它底下的每一個外部節點的路徑,經過的黑色節點數量相同」,還是有點不好判斷。這時候我們先把整棵樹轉為2-3-4樹,此時會有26/2=13個3-節點,要等著我們去建立一棵最大樹高的2-3-4樹。而2-3-4樹的基本要求,是「所有葉節點高度相同」,換個角度去思考,就是所有可以有子節點的地方,都需要補滿才合理。第一層作為根節點,只有一個3-節點,可以有三個子節點。當第二層要有子節點時,就需要補滿,也就是會有3個3-節點,此時對應第三層就可以有九個子節點。當我們將第三層的子節點都補滿時,會有9個3-節點,會剛好把13個3-節點的數量用完,我們會得到一棵高度為3,並且整棵樹都是3-節點的2-3-4樹。最後,再將2-3-4樹還原回紅黑樹,每一個3-節點會變成一個黑色節點跟一個紅色子節點,對高度的貢獻會從原本的1變為2,因此紅黑樹的高度是3*2=6,也就是第15題的正確答案。
- (5 points) Consider a red-black tree with 𝑛 internal nodes, where 𝑛 is even. At most how many of them can be a black node with one red child?
透過這兩題的演練,相信讀者們已經發現,去理解紅黑樹與2-3-4樹的關係,不僅僅是可以協助驗算那麼普通而已。這兩題的觀念,如果只是用紅黑樹的角度去思考,會不容易分析節點個數與樹高的關聯性。但只要把它轉換成2-3-4樹,就會知道題目在問的就是整棵樹都是3-節點的狀況,這兩題就會瞬間變成秒殺題,是不是很神奇呢!
經過了長達三回的篇幅,我們終於將紅黑樹這個大主題給完結了。我們在第一回介紹了紅黑樹的定義,以及如何進行插入;在第二回完整說明刪除該如何進行,並在最終回補上紅黑樹與2-3-4樹的關係,以及透過歷屆試題帶各位讀者活用2-3-4樹的特性。相信這三回都有認真看的大家,都已經成為紅黑樹的大師了吧!那我們就下回再見啦!

