研究所考試

原本筆者是打算接下去講上個月的主題，也就是不同NP完全問題之間的歸約。不過最近各個大學的研究所考試簡章陸續公布，也讓筆者在準備主題的時候想到資工所考試很常考的觀念，也就是紅黑樹（Red Black Tree）。紅黑樹的特性是，他不是很普通的二元搜尋樹，而是在高度上能確保搜尋時間的高度平衡樹，透過顏色和旋轉，讓高度始終維持在 O(log n) 的範圍內。紅黑樹透過嚴謹的性質（例如：根節點為黑、紅節點不能相鄰、每條路徑黑高一致等）確保查詢、插入與刪除操作皆能穩定在對數時間內完成。這種性能穩定性，使紅黑樹成為系統層級資料結構中的重要角色。

在實際應用中，紅黑樹廣泛存在於許多底層實作中，例如 C++ STL 的 std::map 與 std::set，以及 Linux kernel 的排程器、記憶體管理、檔案系統索引，都仰賴其高效查找能力。此外，像是資料庫索引、事件模擬器（event scheduler）、網路路由表、字典結構、甚至語言編譯器的符號表（symbol table）也常選擇紅黑樹作為主要資料儲存結構。由於操作成本穩定、實作複雜度低於 AVL 樹、又能提供良好的最壞情況保證，紅黑樹在「查詢多、更新也頻繁」的場景中特別具有實務價值。接下來，就讓我們來好好瞭解這個很實用也很常出現在考試的資料結構吧！

首先，紅黑樹是一個很特別的資料結構，這裡指的特別是他在不同的原文書裡面，會有不同的定義。紅黑樹顧名思義，就是整顆樹上面會有紅色跟黑色的地方，而根據原文書的不同，紅色跟黑色的地方會不一樣！在Horowitz撰寫的資料結構教材裡，會分為紅色的分支（red branch）以及黑色的分支（black branch）；而在Cormen撰寫的演算法原文書裡，則會分為紅色的節點（red node）以及黑色的節點（black node）。以下會分別說明兩者在定義上的差別。

Horowitz定義（分支區分為紅黑）

• 這棵樹是一棵二元搜尋樹。
• 分支分為紅色的分支（red branch）以及黑色的分支（black branch）。
• 每個節點會有所謂的等級（rank），定義如下：
  • 所有的外部節點（external nodes）的rank為0。
  • 如果parent跟child是以紅色的分支連接，則parent跟child的rank相等（相當於在對應的2-3-4樹中屬於同一個節點）。
  • 如果parent跟child是以黑色的分支連接，則parent的rank為child的rank再加上1（相當於在對應的2-3-4樹中屬於上下節點關係。）
  • 一個內部節點（internal nodes）跟外部節點之間以黑色的分支連接。
• 從根節點到任意外部節點所經過的路徑，不會有連續兩個紅色的分支出現。
• 每個節點的rank的計算方式：從該節點到最近的外部節點，經過的黑色的分支數量。
• 從根節點到每一個外部節點，所經過的黑色的分支數量相等（對應2-3-4樹是B-tree，因此所有葉節點的高度相同）。

Cormen定義（節點分為紅黑）

• 這棵樹是一棵二元搜尋樹。
• 根節點一定是黑色的節點（black node）。
• 所有的外部節點一定是黑色的節點。
• 每一個紅色的節點，其子節點皆為黑色的節點，代表不會有連續兩個紅色的節點。
• 每個節點到他底下的每一個外部節點的路徑，經過的黑色節點數量相同。

可能看到這裡，大家會覺得有一種定義就夠麻煩了，居然還有兩種不同定義？別擔心，這裡告訴大家一個好消息，通常考試會出現的定義，都是以Cormen撰寫的版本為主，也就是把節點分為紅色跟黑色的這個定義。接下來我們會討論該如何對紅黑樹進行操作。

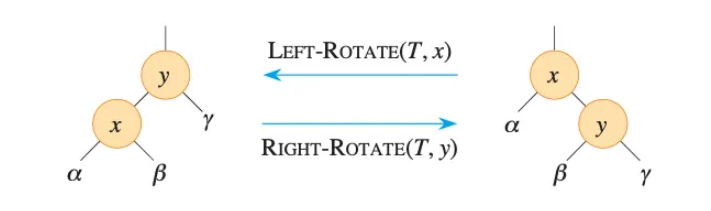
在介紹插入之前，我們要先簡單地說明旋轉的操作。旋轉的目的是在不改變 二元搜尋樹（BST）中序順序的前提下，調整樹形結構的操作，用來維持高度的平衡。旋轉分成左旋轉（Left Rotate）和右旋轉（Right Rotate）：左旋將某個節點 X 向左下方移動，並讓其右子節點 Y 上升成為新的父節點，而他們各自的子節點保持中序順序不變。右旋轉剛好對稱，將某節點 X 向右下移，讓其左子節點 Y 上升，他們各自的子節點保持中序順序不變。

瞭解左右旋轉的操作之後，我們就可以來介紹插入這項操作了：

• 插入的節點固定為紅色的節點。
• 使用(1)顏色轉換(2)左右旋轉來進行調整。

而插入這項操作又可以細分成以下四種狀況：狀況一：插入的節點 Z 為根節點

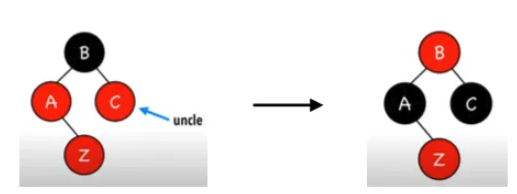
• 將 Z 進行顏色轉換，變為黑色節點即可。

狀況二：插入的節點 Z 的uncle為紅色的節點

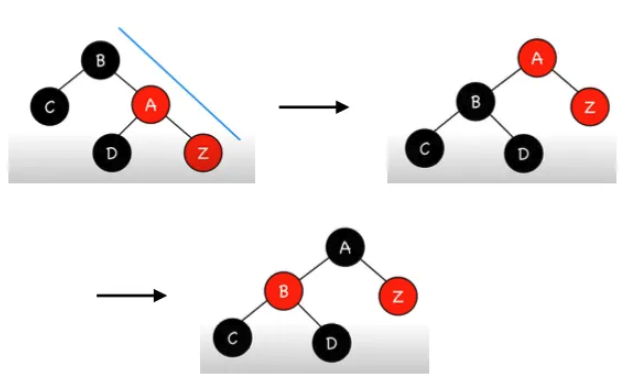
• 直接按照圖示進行顏色轉換：Z節點的上一層節點顏色轉換為黑色，Z節點的上兩層節點顏色轉換為紅色。

狀況三：插入的節點 Z 的uncle為黑色節點(形狀為ㄑ字形)

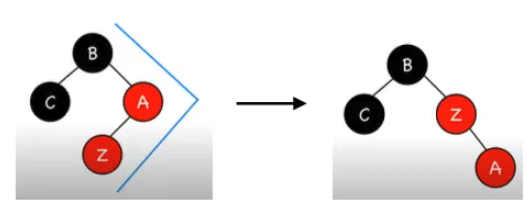
• 形狀為ㄑ字形的意思是，節點Z、節點Z的parent以及節點Z的grandparent呈現ㄑ字型。
• 對節點Z和其parent（節點A）進行旋轉，旋轉方向的判斷方式：選轉後的結果會讓節點Z、節點Z的parent以及節點Z的grandparent呈現一直線，也就是狀況四的樣子。

狀況四：插入的節點 Z 的uncle為黑色節點(形狀為一直線)

• 形狀為一直線的意思是，節點Z、節點Z的parent以及節點Z的grandparent呈現一直線。
• 先對節點Z的parent以及節點Z的grandparent進行旋轉，方向為讓節點Z的parent（節點A）成為節點Z和節點Z的grandparent的根節點。
• 在進行顏色轉換，節點A轉換為黑色的節點，第二層轉換為紅色的節點。

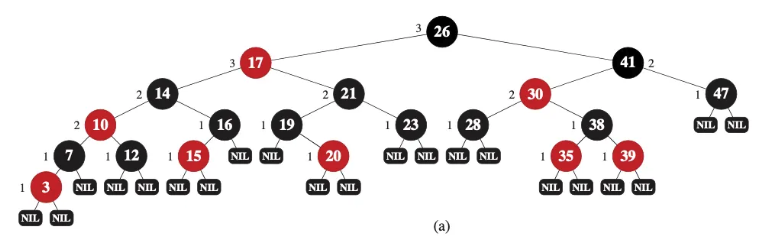
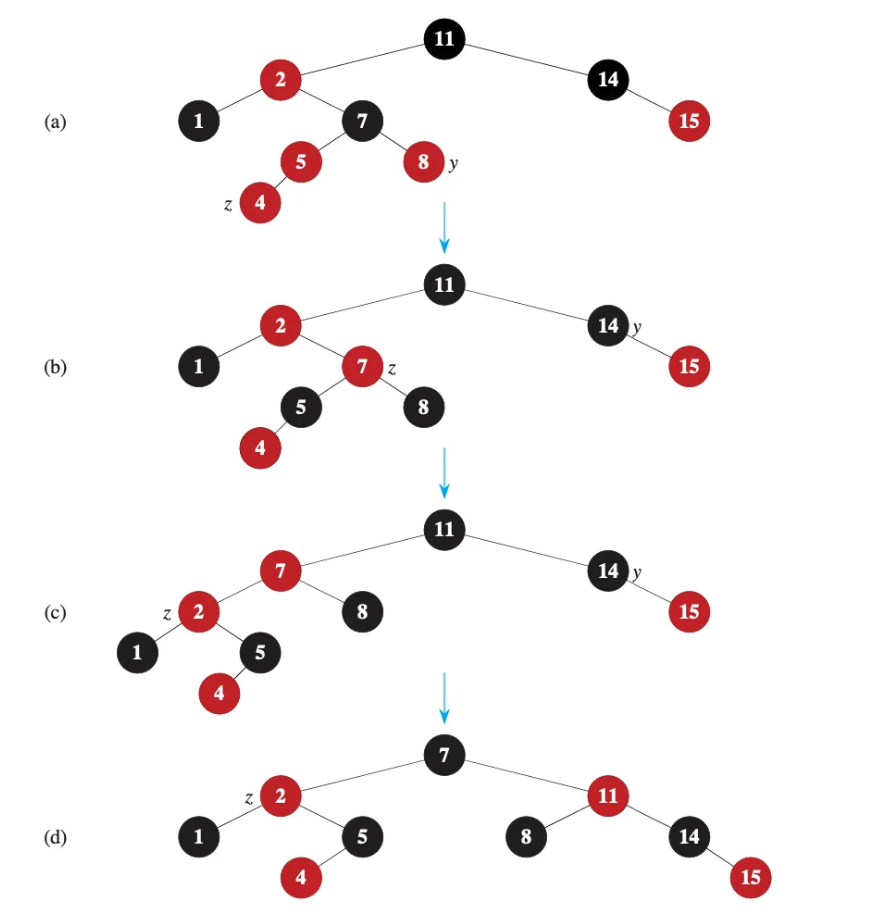
紅黑樹的插入十分複雜，光是狀況就分成四種，還要在裡面進行旋轉跟顏色轉換的操作。在這個範例當中，我們會透過一系列的插入，把剛才介紹的狀況實際演練一遍！

在(a)的這棵紅黑樹上，插入了新的節點（4）。這時候我們要觀察這個節點的uncle，也就是節點8是什麼顏色，來判斷是什麼狀況。因為節點8是紅色，根據剛才介紹的四種狀況分析，是屬於第二種狀況：插入的節點 Z 的uncle為紅色的節點。這個狀況直接進行顏色轉換即可，將節點4的上一層節點顏色轉換為黑色，節點4的上兩層節點顏色轉換為紅色。因此，節點5和節點8都變成黑色，而節點7變成紅色，如圖(b)所示。

但這時候調整還沒有結束，因為顏色轉換讓節點7變成紅色，而其parent也是紅色，違反了紅黑樹不能有連續兩個紅色的節點的定義，因此還需要進行調整！這時候節點Z就會變成我們的節點7，此時要觀察他的uncle，也就是節點14是什麼顏色，來判斷是什麼狀況。節點14是黑色，所以我們知道會是狀況三或四，接著只需要判斷形狀即可。因為節點Z、節點Z的parent以及節點Z的grandparent（節點7、節點2以及節點11）呈現ㄑ字型，所以是狀況三，我們需要進行旋轉，讓他變成狀況四。因此這裡進行左旋轉，讓節點7、節點2以及節點11呈現一直線，如圖(c)所示。

最後，我們需要把狀況四解除，因此我們會需要進行右旋轉，將節點7變為節點2和節點11的根節點。旋轉完成後，還需要進行顏色調整，最上層的節點7轉為黑色，下面一層的節點2和節點11轉為紅色，如圖d)所示。此時，已經沒有違反紅黑樹定義的情況發生了，因此本次插入也就順利完成了！

紅黑樹作為2-3-4樹的二元搜尋樹版本，在實作上能夠使很多操作的時間複雜度降低，因此是許多系統底層元件的核心資料結構，無論是 STL、作業系統核心，或資料庫索引，都能見到它的身影。礙於篇幅緣故，本次專欄只來得及介紹紅黑樹的定義以及插入的操作方式。在下一回的專欄裡，筆者會介紹紅黑樹的刪除操作，以及從歷屆試題裡找出一些經典題型，讓各位讀者能對紅黑樹有更全面的認識。