研究所考試

在上一篇我們介紹了紅黑樹的特性，相較於一般的二元搜尋樹，紅黑樹透過顏色和旋轉，讓高度始終維持在 O(log n) 的範圍內。我們首先介紹了紅黑樹在Horowitz撰寫的資料結構原文書以及Cormen撰寫的演算法原文書裡不同的定義，並以較常用於考試的Cormen定義，也就是分為紅色的節點（red node）以及黑色的節點（black node）的版本來說明如何進行紅黑樹的插入。

在本次的文章裡，我們要來完整介紹紅黑樹是如何進行刪除。先有個簡單的概念：紅黑樹的刪除操作，是先依照二元搜尋樹的方式移除節點，再視被刪除節點的顏色決定是否進行修正（delete_fixup）。若刪除的是紅色節點，樹的性質不受影響；但若刪除黑色節點，可能造成黑高不一致，也就是違反「每個節點到他底下的每一個外部節點的路徑，經過的黑色節點數量相同」這個特性，需透過顏色調整與旋轉來補回黑高。透過delete_fixup這項操作進行修正，得以確保紅黑樹在刪除後仍能維持高度平衡，讓後續的操作依然能在對數時間內達成。

首先，我們先來複習一下在Cormen撰寫的演算法原文書裡，紅黑樹是如何被定義的：

Cormen定義（節點分為紅黑）

• 這棵樹是一棵二元搜尋樹。
• 根節點一定是黑色的節點（black node）。
• 所有的外部節點一定是黑色的節點。
• 每一個紅色的節點，其子節點皆為黑色的節點，代表不會有連續兩個紅色的節點。
• 每個節點到他底下的每一個外部節點的路徑，經過的黑色節點數量相同。

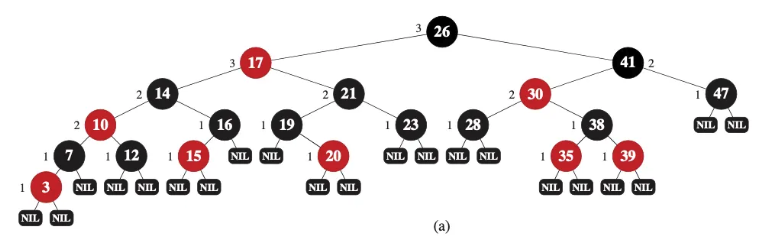
紅黑樹的刪除大致上可以分為兩個步驟，首先是先處理刪除節點的部分，這個部分與正常的二元搜尋樹刪除的步驟相似，目的是要先讓刪除完的樹有一個初步的形狀。但因為我們在處理的是紅黑樹，必須在刪除的同時確保符合定義，也就是從根節點到所有的外部節點經過的黑色節點數量相同，因此會需要進行delete_fixup來修正整棵二元樹。再開始介紹如何刪除以前，我們要先來介紹transplant這項操作：

操作介紹：transplant

在刪除的操作裡，我們會需要知道被刪除的點該如何從原本的樹裡面被拿出來，以及他原本的parent跟children該如何處理。因此會有兩個主角，分別是節點u和節點v，原則就是將節點u的parent跟children妥善安排到節點v上面，就可以安心將節點u刪除了。首先我們先來看在原文書裡如何定義transplant這項操作：

首先我們會先判斷u節點的狀況，分成三種：

1. 當u節點是整棵樹的根節點時：將整棵樹的根節點設為v節點。
2. 當u節點是其parent的左側節點時：將其parent的左側節點設為v節點。
3. 當u節點是其parent的右側節點時：將其parent的右側節點設為v節點。

進行完以上判斷後（1~5行），我們已經成功把u節點的parent和children關係都轉給v節點了，最後（第6行）再告訴整棵樹，u節點的parent已經正式變為v節點的parent，就大功告成了！

接下來，我們先來看在Cormen原文書裡如何定義刪除的演算法：

我們先專注於整個刪除的部分（3~20行），可以分為三個狀況：

狀況一：刪除的節點 Z 左側child為NIL

1. 呼叫transplant(z, z.right)，用節點z的右側節點來取代節點z：

狀況二：刪除的節點 Z 右側child為NIL

2. 呼叫transplant(z, z.left)，用節點z的左側節點來取代節點z：

狀況三：刪除的節點 Z 的兩側children皆不為NIL

3. 找到節點z右子樹中的最小值，標記為y，並記錄其顏色（delete_fixup要用到）
4. 將節點y的右側節點標記為x，呼叫transplant(y, x)

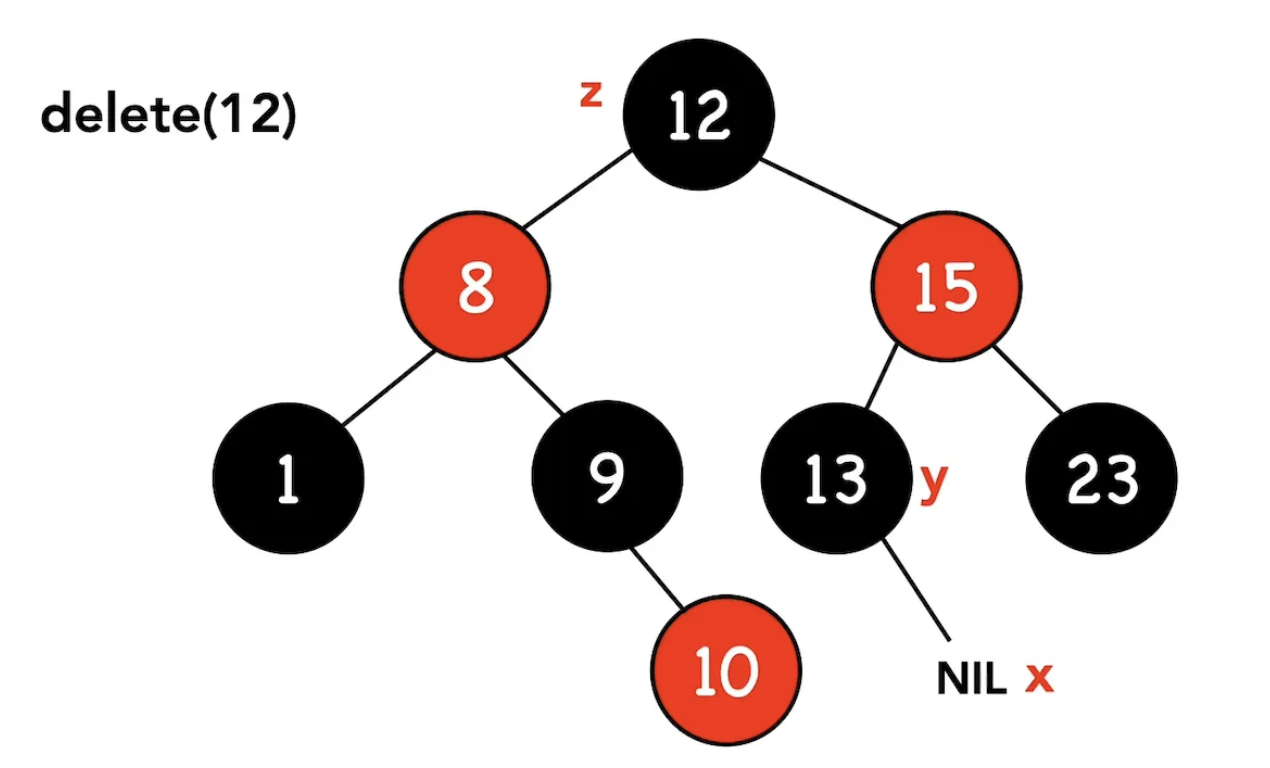
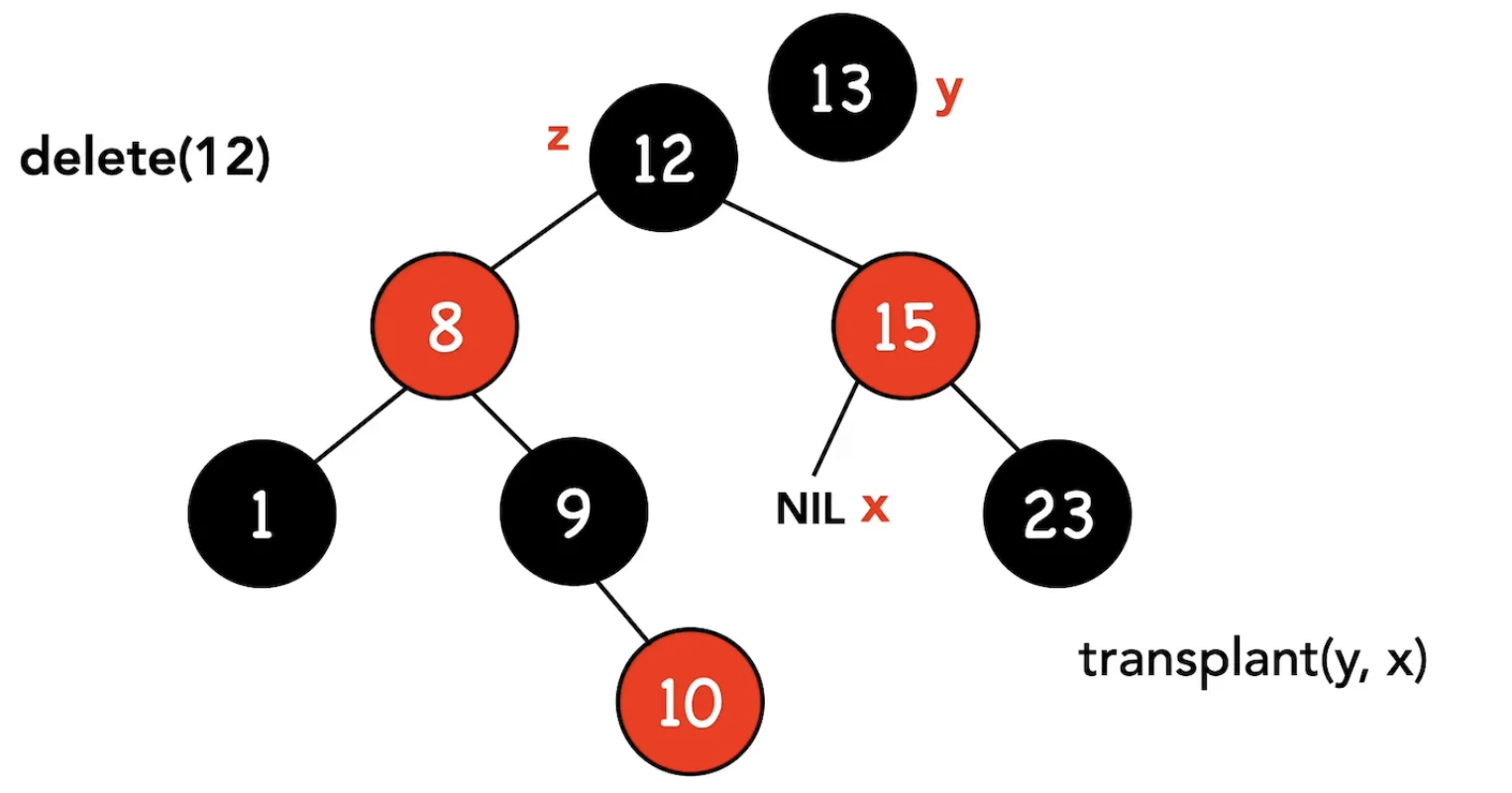
5. 節點y跟節點z的右側子樹建立連結（y.right＝z.right；y.right.p＝y）
6. 呼叫transplant(z, y)：把節點z刪掉後將z.left接到y.left

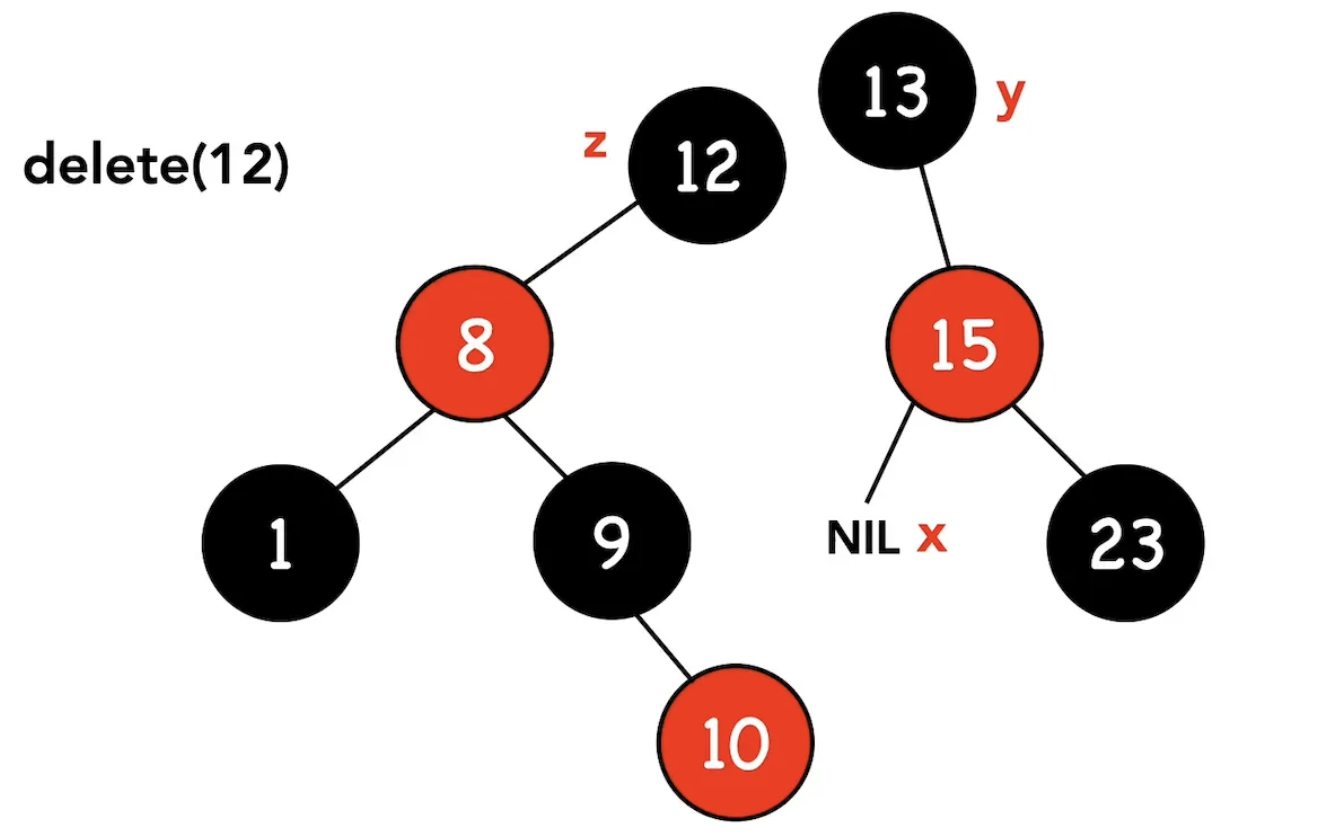
講解到這裡並配合說明圖片去看，相信有不少讀者已經發現，這樣的操作不就是二元搜尋樹在進行刪除時的操作嗎！那為什麼要講得那麼複雜？原因是因為，在紅黑樹的刪除裡，存在delete_fixup這項維持紅黑樹特性的操作，而在進行這項操作時會需要參考節點y的顏色作為依據。因此除了原本的刪除流程以外，我們會需要去追蹤節點y的顏色，以判斷是否需要做最後的調整！

最後，我們就來看紅黑樹刪除的大魔王，也就是delete_fixup該如何操作吧：

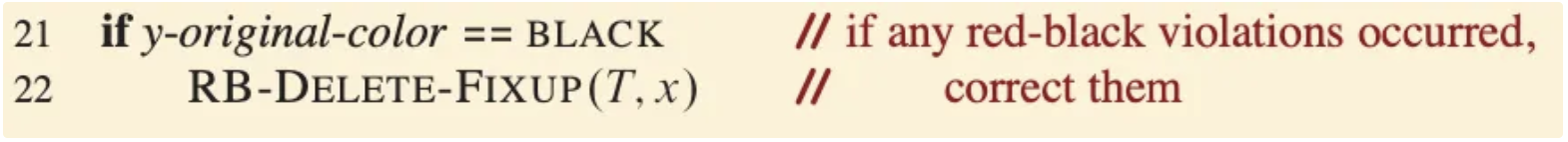
規則很簡單，如果y-originall-color是黑色，就對節點x進行在delete_fixup這項操作。以下操作中的節點x，代表著高度出問題的節點，而節點w代表節點x的sibling，兩者關係為節點x是左側節點，分為四種狀況：

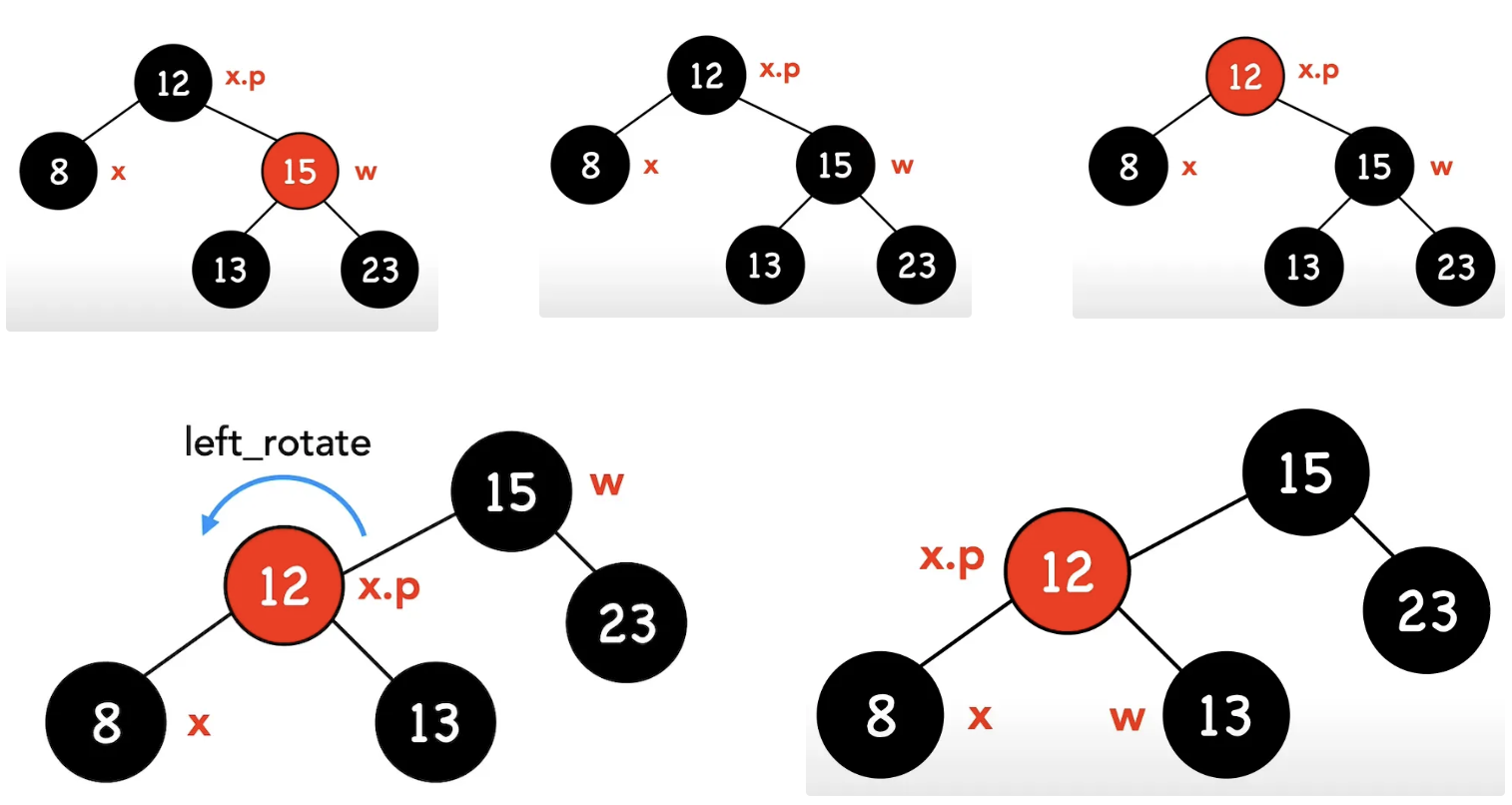
狀況一：節點 w 是紅色節點

1. 將節點w設為黑色節點
2. 將節點x的parent設為紅色節點
3. 對節點x的parent做左旋轉
4. w = x.p.right，轉為其他狀況繼續操作

狀況二：節點 w 是黑色節點，且其左右children皆為黑色節點

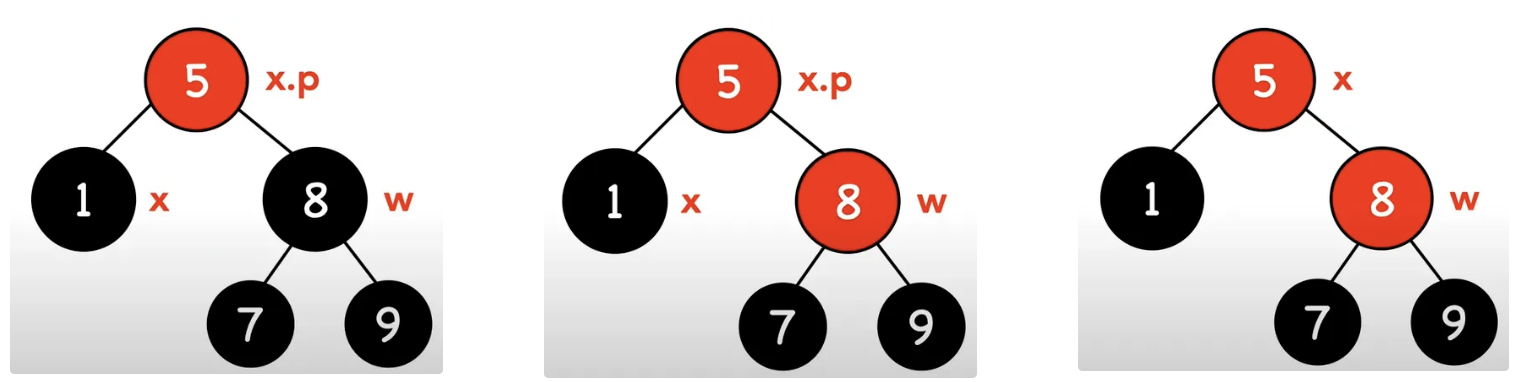
1. 將節點w設為紅色節點
2. x = x.p，向上繼續操作

狀況三：節點 w 是黑色節點，其左側child為紅色節點，右側child為黑色節點

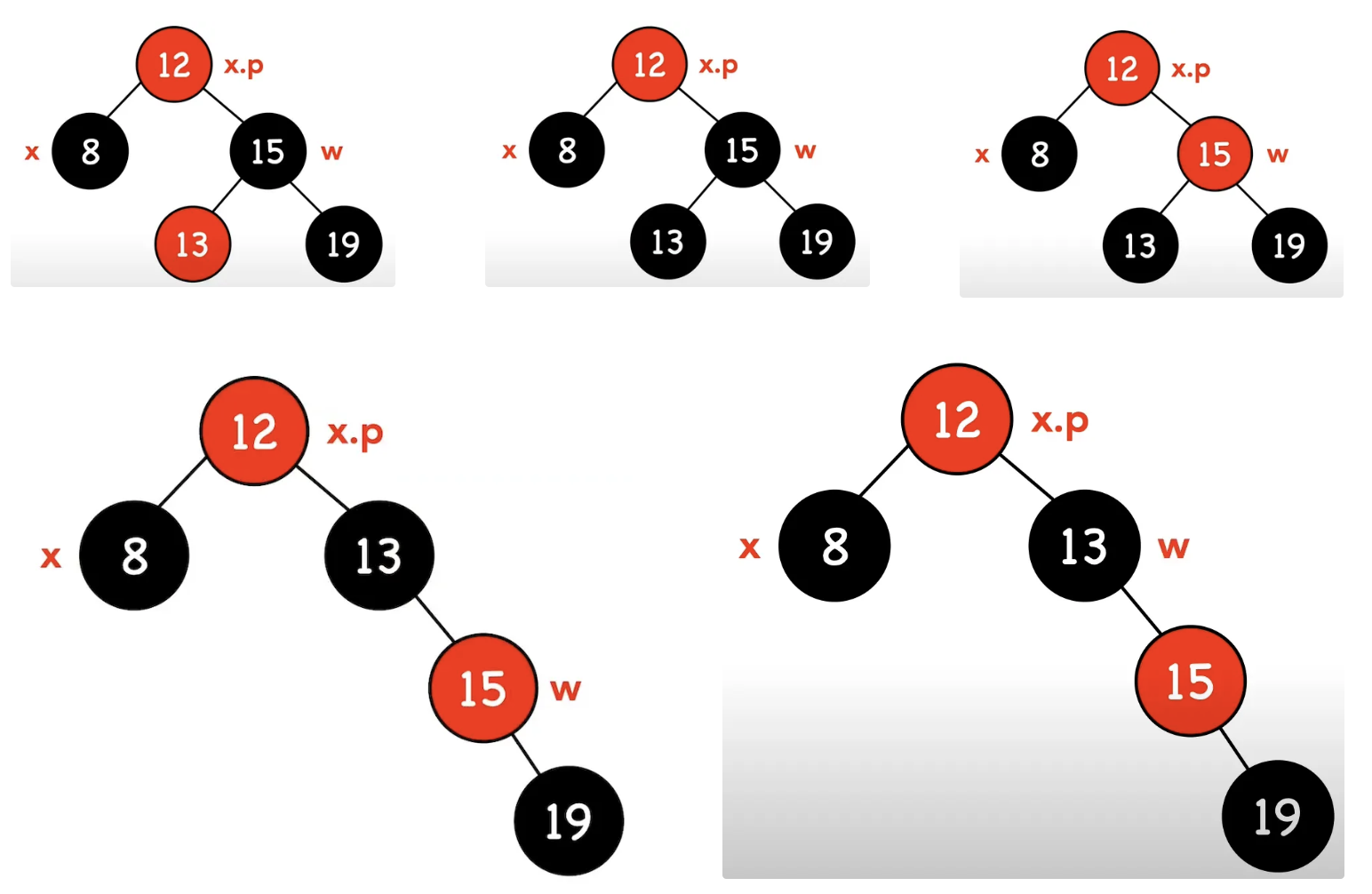
1. 將節點w的左側節點設為黑色節點
2. 將節點w設為紅色節點
3. 對節點w做右旋轉
4. w = x.p.right，轉為其他狀況繼續操作

狀況四：節點 w 是黑色節點，右側child為紅色節點

1. 將節點w設為節點x的parent的顏色
2. 將節點x的parent設為黑色節點
3. 將節點w的右側節點設為黑色節點
4. 對節點x的parent做右旋轉
5. 將節點x設為整棵樹的根節點

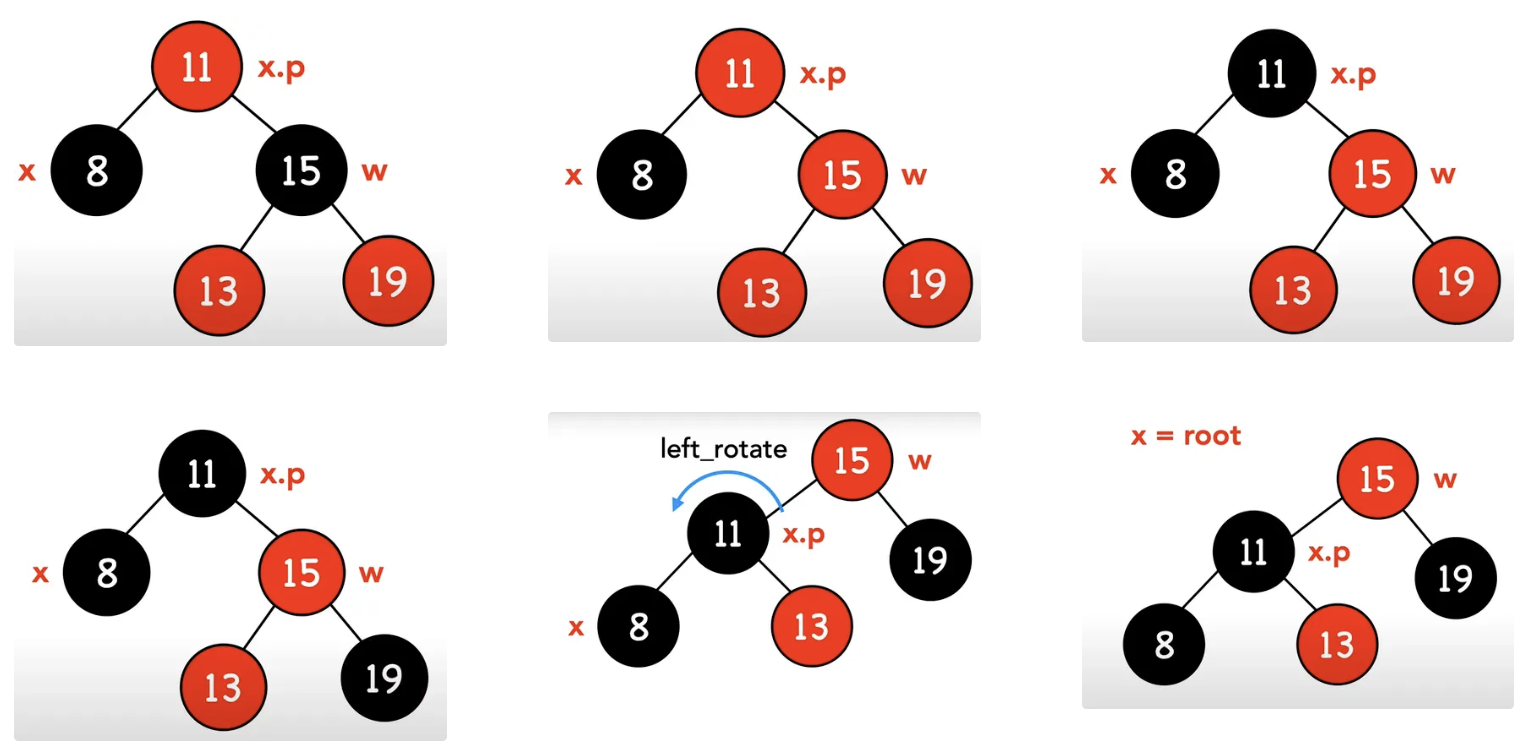
最後的最後，確保節點x是黑色，根節點也是黑色，紅黑樹的刪除就大功告成了！

總結而言，紅黑樹的刪除可視為「先處理結構、再維持紅黑樹性質」的兩階段流程。首先依循二元搜尋樹的刪除規則，將欲刪節點轉換為刪除至多只有一個子節點的情況，並以後繼節點取代之。接著，關鍵在於判斷實際被刪除節點的顏色：若為紅色，紅黑樹性質自然維持；若為黑色，則可能導致黑高不足，需進行刪除修正程序（delete_fixup）。修正過程透過檢視兄弟節點與其子節點的顏色，搭配顏色變換與旋轉操作，逐步消除黑高有問題的情況，直到紅黑樹的所有性質重新成立。透過這套嚴謹的步驟，紅黑樹在刪除後仍能保持高度平衡，並確保操作時間維持在對數時間裡。因為紅黑樹的刪除確實是個大工程，礙於篇幅緣故本次專欄只來得及介紹完紅黑樹的刪除步驟及演算法流程，看來是需要在花一篇紅黑樹(3)來對紅黑樹進行完整的總結，以及透過歷屆試題帶大家了解紅黑樹會如何出現在考題中。那我們就下回再見！