一開始，我們先來複習一下，你還記得什麼是齊次函數嗎？什麼又是正向單調轉換呢？如果忘記你就完全翻一下，我們把兩件事的特色合在一起，你知道會如何嗎？齊序函數會有什麼特性呢？我們今天的重點就是，到底齊序函數會有什麼特性呢？

我們學到的正向單調轉換很神奇，他是不會改變函數值的「序列」，那麼你學過的無異曲線就可以拿出來用了，什麼是無異曲線？就是那些滿足程度「一樣好」的商品組合們，連起來的一條線對嗎？那正向單調轉換，會讓「一樣好」的組合們，變成「不一樣好」嗎？當然不會呀，因為正向單調轉換並不改變函數值的序列對嗎？那正向單調轉換，會改變無異曲線的樣子嗎？當然就不會摟！這是最大的重點了！

如果我們把齊次函數（例如U = xy）進行正向單調轉換（例如平方），那麼新的函數叫做齊序函數（U = x²y²），他們兩個畫出來的無異曲線會怎樣？形狀一定完全一模一樣！因為一樣好的組合們被你畫了線，轉換完後這些組合也都還是一樣好，無異曲線的「形狀」，本來就是描著那些一樣好的商品組合畫出來的，轉換後一樣好，無異曲線當然就會長完全一樣。所以齊次函數畫出來的無異曲線有什麼特性，齊序函數一定都會有的，因為他們的形狀完全一樣呀！

那麼齊次函數的無異曲線有什麼特點？

最大的特色，就在於它的邊際替代率MRS，一定可以寫成兩個變數比值的相關函數了，例如U = xy是個齊次函數，他的MRS = y/x；U = x² + y²，他的MRS = x/y，這又表示什麼，表示只要x,y商品數量的比值固定，對這一組齊次函數而言，例如下圖，當y/x固定為a或b，必定就是一條從原點發射的射線，這一條射線遇到無異曲線的點們，你可以看到他們切線斜率都相同，也就是MRS一定都相等了，所以他們的無異曲線看起來，就會排得「很好」、很「整齊」，很像等比例往外放大一樣，等等，所以你現在看到這個整齊的性質，是齊次函數有的？還是齊序函數有的呢？

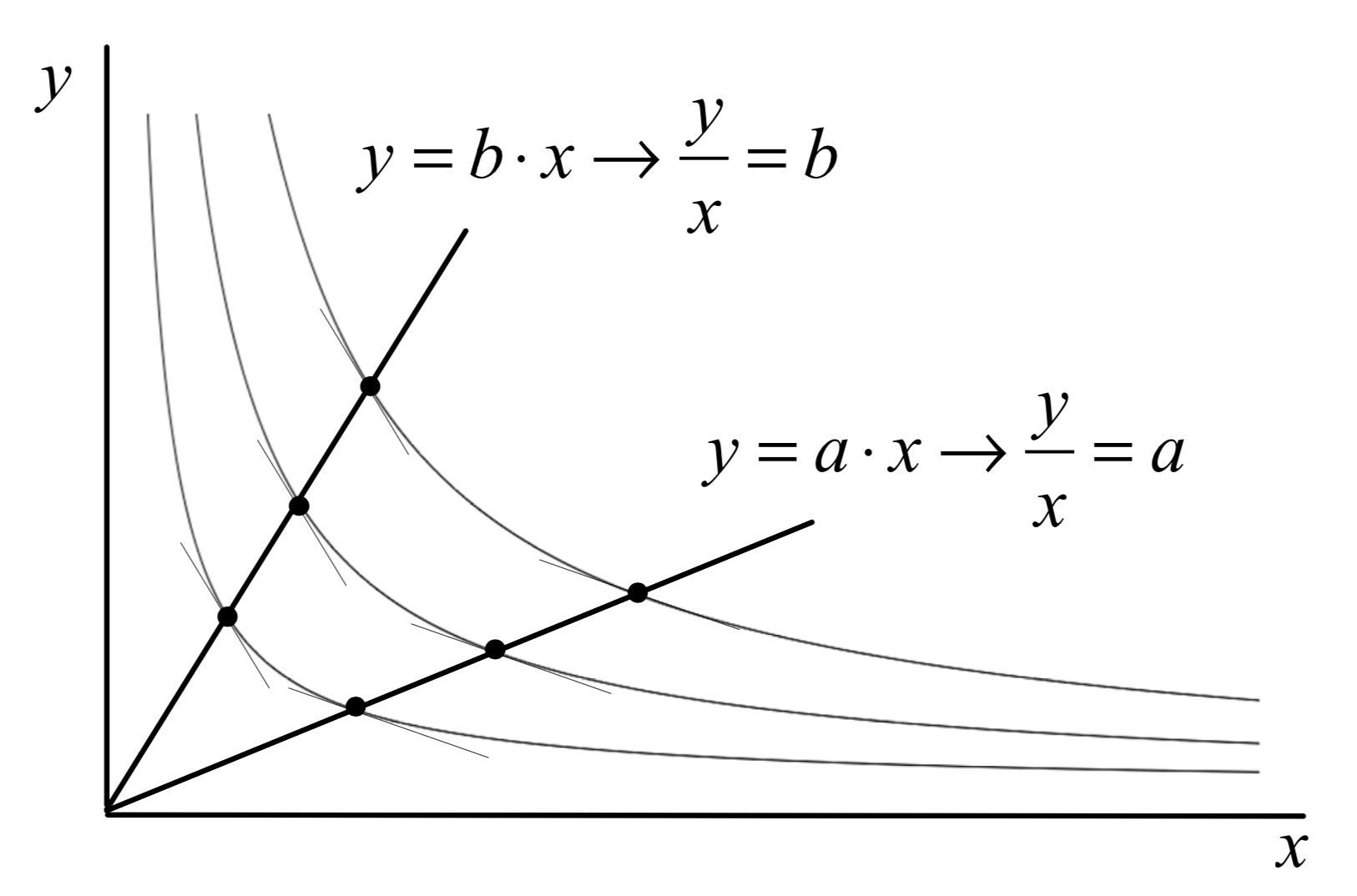
沒錯！只要齊次有的無異曲線性質，在正向轉換後的齊序函數身上，必定都會看得到，所以「從原點發射的射線，遇到等值曲線（無異曲線）的切線斜率都相等」的這個性質，你一定可以在齊次函數，以及齊序函數身上看得到，那要是我看到這個性質發生了，我能不能回頭判斷，討論的函數一定是齊次還是齊序呢？

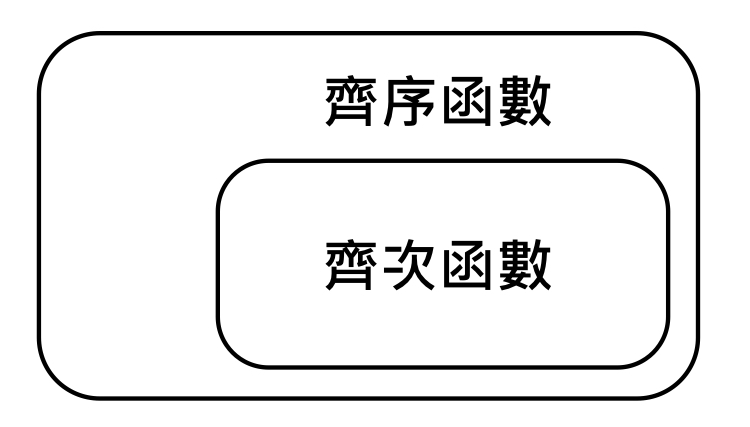
我要提醒你一件事，正向單調轉換的方式很多，我們有說過齊次函數本身已經必定是齊序函數了，但有沒有可能把齊次轉換完就不是齊次了呢？當然有可能呀，我們隨便加一個常數，他就不是齊次了，但是他卻一定是齊序函數！所以我們敢保證齊次函數一定是齊序函數，但是不敢保證齊序函數一定還是齊次函數，既然「齊次必為齊序，齊序不一定為齊次」，我們做了一個圖在下面，幫助你有印象。

好的，你差不多要暈了，我們統整一下今天的目標和重點，我們今天要知道「齊序函數的特性」，我們用三個階段來學：

想法1.正向單調轉換不會改變無異曲線的特性

想法2.齊次函數的無異曲線有一種特性，從原點發射的射線，遇到等值曲線的切線斜率都相同，因為他的MRS都會是變數比值的函數。

想法3.正向單調轉換會把齊次函數的特性，繼承到齊序函數身上，但是轉換完成之後的新函數，我們只能保證他一定可以叫做齊序函數，但是也許他可能已經不是齊次函數了。

「齊次必為齊序，齊序不一定為齊次」的話，「從原點發射的射線，遇到等值曲線的切線斜率都相同」的這個特性，是齊次函數「才」有，還是齊序函數「就」有了呢？我們會說，只要是齊序函數，就有這樣的特性了，所以我們只要看到：「從原點發射的射線，遇到等值曲線的切線斜率都相同，也就是MRS都會是變數比值的函數。」這保證一定是齊序函數，但我們不敢說他一定齊次，而這個性質我們就叫他「齊序性質」。