我們學了三個重要的概念：「齊次函數」、「正向單調轉換」、「齊序函數」，前兩個概念你應該都有快速的判斷方法了，而我們花了三次的篇幅講的「齊序函數」，是不是也有快速的判斷方法呢？

依照上週講的特性－「齊序性質」，我們知道齊序函數在平面上所畫出來的等值曲線，和從原點發射的射線交點，切線斜率都必定會相等。而我們在個體經濟學中，「齊序性質」這個概念最常被討論在消費者的「效用函數」與生產者的「生產函數」上，尤其是生產函數用得更多！如果效用函數是齊序，或是生產函數是齊序，那會怎麼樣呢？

我們把效用函數畫在二維平面上，呈現出來的是無異曲線，而生產函數在二維平面上畫出來的則是等產量曲線，無異曲線的切線斜率受到MRS影響，而等產量曲線的切線斜率則取決於MRTS，那從原點發射的射線呢？

舉例來說，回憶一下上週的圖，如果我們討論下圖中這些畫在xy平面上的無異曲線們，只要有一組效用函數，我們就可以畫出無限多條無異曲線，我們隨便畫了其中的三條無異曲線出來看看。

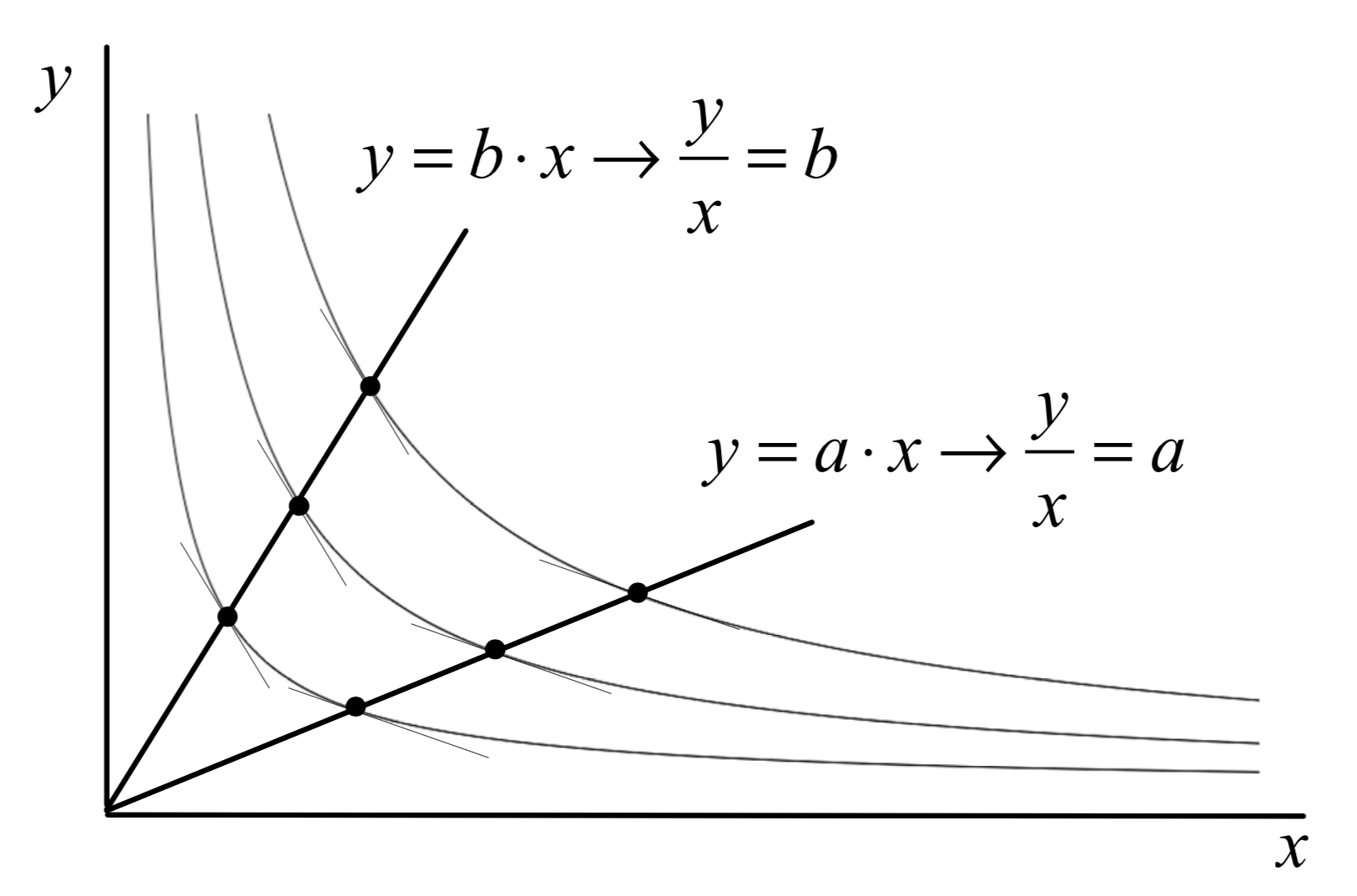
你可以在上圖中發現，任何一條從原點發射的射線，都能表達成 y = ax 或 y = bx 的型態，也就表示 y / x = a 或 y / x = b，因為射線上的任意點都能用座標表示，我們把座標中的 x, y 變數相除，同條線上的變數比值絕對是固定的，例如(x, y) = (1, 2)，這個點一定位於 y = 2x 這條射線上，而 y / x 當然就等於 2。

然後呢？到底要說什麼呢？我想說的是，這條射線上遇到無異曲線的點們，在無異曲線上的切線斜率都相同，那切線斜率又被MRS影響，只要MRS都相同，切線斜率就必定相同了，又因為點在射線上，變數比值也都相同，我們把這些想法串起來，會變成怎麼樣呢？

只要是齊序的效用函數，會符合齊序性質，而齊序性質就是從原點發射的射線，遇到的MRS都會相同，只要在相同射線上，座標中的變數比值（x / y 或 y / x）就固定，而MRS也固定，只要在不同射線上，變數的比值就會不同，而MRS也就跟著改變，那不就表示，齊序效用函數畫的無異曲線，他的MRS根本就會是變數比值（x / y 或 y / x）的函數了！只要給我們一個變數比值，我們就可以對應出一個MRS，只要有固定的比值，那就會有固定的MRS，而無異曲線切線斜率就都相同了。

如果套用到齊序的生產函數呢？只要生產函數是齊序，他等產量曲線上的MRTS就會被變數比值（K / L 或 L / K）決定，也就必定是MRTS會是變數比值（K / L 或 L / K）的函數呢！而這也就是我們判斷齊序函數的方法了！只要我們遇到一組函數想判斷是否齊序，我們只需要計算他的 MRS 或 MRTS，如果算出來是變數比值的函數，那這個函數就必定是齊序函數，因為我們保證他會符合「齊序性質」！

我們試試看，請問你，如果有一個效用函數 U = xy，這個效用函數是齊序嗎？當然是，以前我們學的是，因為他是齊次函數所以他一定是就是齊序函數了，那用我們今天學的方法呢？我們算一下他的 MRS = MUx / MUy = y / x，你發現他的MRS是變數比值的函數，只要變數比值固定，MRS就固定了，所以他當然就是齊序函數，這就是齊序的判斷方法！

留兩個函數給你，你可以試試看嗎？請問生產函數 Q = L²K³、Q = 2L + 3K，這兩個生產函數是齊序函數嗎？