峰態係數用來衡量資料的峰態 , 確認資料是否有離群值。峰態係數的定義為

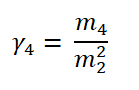
其中

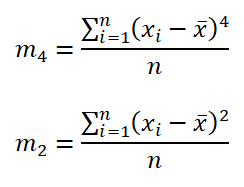
常態分配的峰態係數是 3，若以 Z 分數作為判斷離群值的依據，則當 Z 分數大於 3 或小於 -3，可視作該資料為離群值。而根據常態分配的累積機率分配表，可以得知，表示出現離群值的機率為2×0.00135=0.0027。若資料的峰態係數大於 3，則可解讀為出現離群值的機率比常態分配更高；若資料的峰態係數小於 3，則出現離群值的機率比常態分配更低。例如利用 1983M1:2025M2 的台幣即期匯率變動率，所計算出來的峰態係數為6.90，而出現離群值的機率為0.0121。若利用1948Q1:2024Q1的美國實質 GDP 年增率計算出的峰態係數為4.64，而出現離群值的機率為0.0098。

若使用 2015M3:2025M3的S&P500 日報酬率作計算，其峰態係數為 17.75，出現離群值的機率為0.0140。看起來S&P500的峰態係數很大，但是出現離群值的機率沒有大很多，此時可以從出現的離群值大小去解釋，即出現的極端離群值的數字大小越大，其峰態係數越大。S&P500的Z值最大為8.27，最小值為 -10.67；而台幣即期匯率變動率Z值最大為5.70，最小值為 -4.39。同學如果對於計算上有興趣，可以到 FRED (Federal Reserve Economic Data) 網站下自由下載資料後去練習。