【推薦書籍】
統計學(含概要)歷屆試題詳解、
統計學:重點觀念與題解(上) 、統計學:重點觀念與題解(下) 、計量經濟學與財務工程、
統計學精選666題
【推薦課程】
行動版、數位課程
篇名
分析113年台大財金甲丙考題(經濟分析)
作者
許誠哲
說明
發佈時間:20241230
在這次的專欄中,我將介紹113台大財金甲丙中,一題結合賽局與統計學期望值的題目。題目如下:
【甲有一間房子要出售,其可選擇自己賣或賣給乙。若甲自己賣,則扣除所有因賣房而產生的費用後,賣房淨收入將為V。甲除非經 歷自己賣房子的過程,否則其不知V確實的值,而僅知V的分配為介於1,200萬元與3,600萬元之間的均等分配(Uniform distribution)。 乙為專業房產投資人,其始終知道V確實的值,且該房若由乙來賣,則扣除所有因賣房而產生的費用後,賣房淨收入將為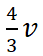 。
。
賽局 進行如下。(i)甲決定一售價P並告知乙。決定P時,甲僅知V的分配而不知V確實的值。(ii)乙決定是否以P的價格向甲購買該房後再 賣出。若乙買,則甲與乙的報酬分別為P與 V-P。若乙不買,則甲自己賣,此時甲與乙的報酬分別為V與0。參賽者均極大化自己的期望報酬。對甲最適的P為___萬元。均衡時甲的期望報酬為___萬元。】
為了方便解說,令屋主為題目中的甲,房仲為題目中的乙。對於房仲來說,只要屋主訂的價格 p < 4v/3,意即 v > 0.75p,則有利可圖。因此若 v < 0.75p,則屋主可獲得 v 的價值,而若 v > 0.75p,屋主可獲得 p 的價值。圖示如下
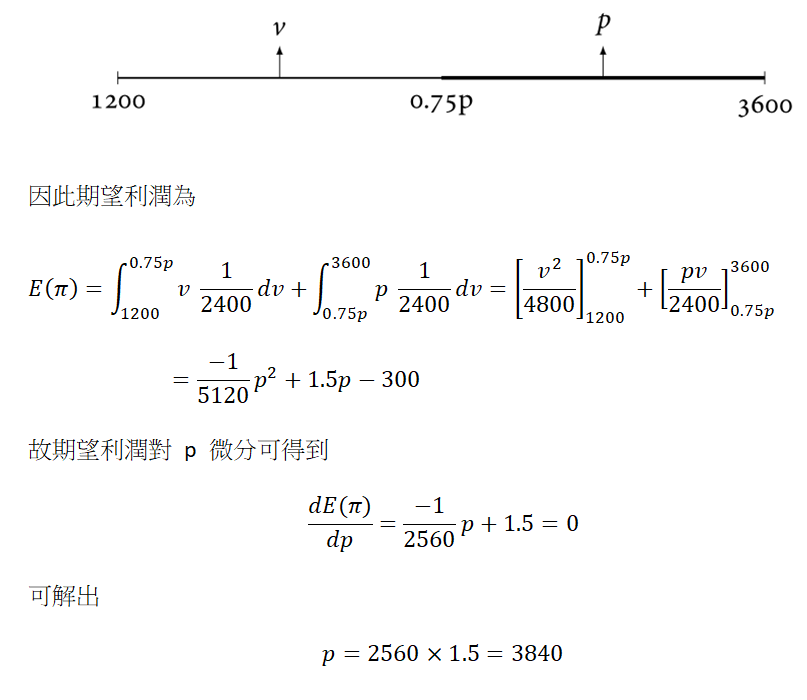
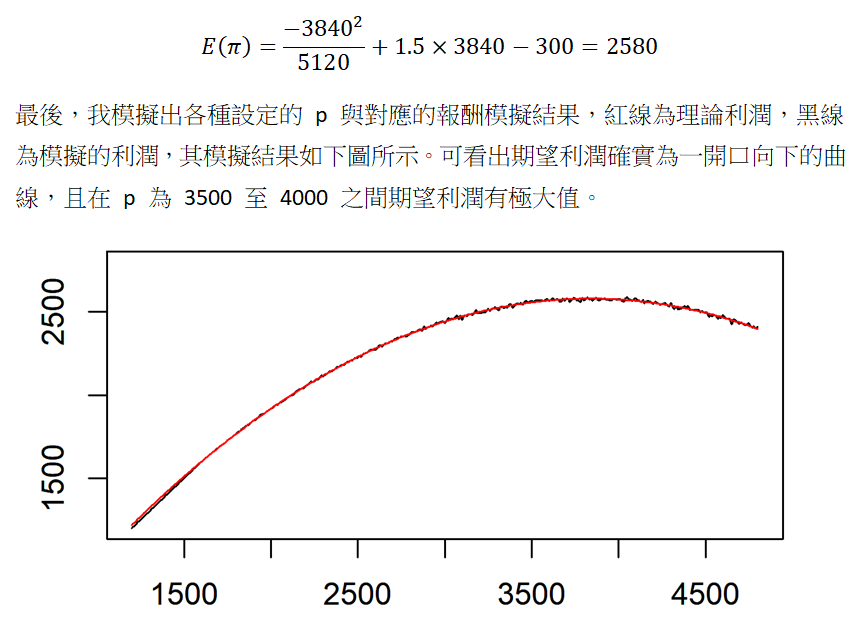
關鍵詞
統計學、期望報酬、期望利潤
刊名
商研所許誠哲
該期刊-上一篇
該期刊-下一篇

