想像一下, 若你是研究所入學的面試官, 有兩位學生 (稱之為學生 A 與學生 B) 來自於不同國家的不同學校。在同樣的課程中, 若學生 A 的成績為 85 分, 學生 B 的成績為 90 分, 你認為學生 A 的表現比較好, 還是學生 B 的表現比較好?一般來說, 面試官傾向找出在該群體中相對表現較佳的學生, 但若只看到百分制成績上的數字, 無法看出學生的相對表現。因為百分制的分數會受到教授給分偏好(偏甜或偏硬)或者分數計算上(是否會調分)的影響, 此時 T 分數就是一個很好的相對表現衡量。

在介紹 T 分數之前, 我們先介紹 Z 分數 (Z-score)。 Z 分數的計算方式為

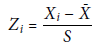
其中Xi是第 i 位同學的成績,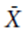與S分別表示全體學生的平均與標準差。因此若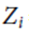=2表示該位同學的成績比平均高了 2 個標準差, 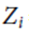=-1則表示該位同學比平均低了 1 個標準差。簡單的說, 若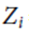越大則表示該位同學的相對表現越佳, 因此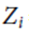又稱作標準化分數 (standardize score)。為了使得標準化分數貼近百分制分數, T分數即為將 Z分數進行線性轉換, 即

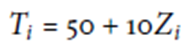
意即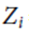=2 則對應到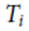= 70, 且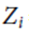= -1 則對應到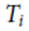= 40。經過T分數的換算之後, T分數的平均為 50 分, 標準差則為 10 分。且T分數的計算基準是同一個群體的所有學生, 因此我們可以從不同學生的T分數直接看出該學生在所處群體的相對表現如何。若群體的學生數夠多且分佈近似於常態分配的鐘型曲線, 我們可以由常態分配的機率得知 P(T > 70) = P(Z > 2) = 0.0228, 意即僅有2.28% 的學生其 T 分數會大於 2,至於 T 分數大於 80 或者 Z 分數大於 3 的情況就更為少見了, 約只有 0.13% 的比例。

 T分配或類似的概念在實際生活的應用相當多。舉例來說, 日本升學補習班衡量學生成績相對表現的「偏差值」就是T分數。知名學府如東大、慶應與早稻田的偏差值大多在70分左右, 意即需要比平均高於2個標準差, 或者位於全部考生的前 2%。美國職棒大聯盟的球探對於該位球員的表現會給予20-80區間的分數: 20-30分是遠低於平均水準, 50分是大聯盟平均水準, 而70-80分是遠高於平均水準。研究所入學考試中, 若考試可以選擇考科 (例如可選考統計或者微積分), 為了比較不同考科成績的相對高低, 其成績計算方式會使用 T 分數。若除了筆試以外亦有口試, 因為口試的分數平均會較高 (分數約在60-80) 間較常見, 因此會將選考的考科的分數調整至平均數為70, 標準差為10, 意即

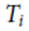= 70 + 10。

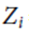當然, 除了 T 分數外也有其他種相對表現給分標準, 例如等第制或者直接加註該科成績相對位置的百分比。但是等第制成績僅將所有的學生分成 10 個等級 (A+, A, A-, B+, B, B-, C+, C, C-, F), 在給分時學生常有爭議。舉例來說, A+ 的最後一位同學與 A 的第一位同學分數或者相對表現可能差異很小, 但在等第上缺差了一個等級, 這是分級較少衍生的問題。但由於 T 分數理論上可以無限細分, 又可以直接看出相對表現且計算方便, 且教授給分仍可使用習慣的百分制, 因此在這幾年有部分大學成績單會加註, 我認為也應該是未來評分標準的趨勢。