研究所考試

在許多現代化系統中，如何有效地將一組任務分派到多台機器或處理單元，是一個攸關效能的核心議題。無論是在雲端運算、資料中心、製造流程，或是多核心處理器上，資源的合理排程直接決定了系統的整體生產力。Makespan Minimization（最小完工時間問題）便是此領域中最經典、最具代表性的問題之一，而 LPT（Longest Processing Time first） 演算法則是解決此問題時最廣為人知的啟發式方法。

基本定義

Makespan Minimization 問題指的是：給定 n 個作業（jobs），每個作業 j 有固定的處理時間 p_j，以及 m 台平行且相同的機器（machines）。目標是在不允許任務中斷的前提下，將作業分配給機器，使所有作業完成的最晚時間（完工時間最大值），也就是 makespan，達到最小化。

數學上，常將該問題記為：P||C_max。
其中 P 表示「identical parallel machines」（同質平行機器），C_max 則是 makespan。

問題性質

當 m=1 時，問題退化為單機排程，makespan 即為所有作業處理時間總和，求解容易。
當 m≥2 時，問題屬於 NP-hard，也就是沒有已知的多項式時間演算法能保證求得最優解（除非 P = NP）。

因此，研究者通常尋求精確演算法（Exact algorithms），例如分枝限界（Branch and Bound）、動態規劃（Dynamic Programming）等方法，適合小型實例。啟發式（Heuristic）與近似演算法（Approximation algorithms），可在合理時間內產生近似最優解，適合大規模情境。

解決 makespan 問題時，通常會先計算一個 下界（lower bound），以評估演算法結果的品質。常見下界包括：

即使有下界，由於組合空間龐大，直接窮舉所有作業分配方式不切實際，這也是 LPT 等啟發式演算法發揮價值的原因。

核心概念

LPT（Longest Processing Time first）是 Graham（1969）提出的一種簡潔貪婪法，透過「優先處理長作業」的策略，試圖避免負載過於不平衡。其核心概念是：長作業若安排過晚，可能導致 makespan 顯著增加，因此應儘早分配。

演算法步驟

1. 排序：將所有作業依處理時間 p_j 由大到小排序。
2. 分派：依序將作業分配到目前總負載最小的機器上。
3. 重複：直到所有作業都被安排完成。

LPT 的總時間複雜度為：O(nlogn+nlogm)

其中 O(nlogn) 來源於「將所有作業依處理時間遞減排序」的步驟，常用的排序演算法如 Merge Sort、Heap Sort 或 Quick Sort（平均情況） 都能達成此複雜度。排序完成後，我們需依序將每個作業分派至當前負載最小的機器。若直接線性掃描 m 台機器，每次分派需 O(m)，總計 O(nm)，在機器數龐大時效率不佳。為改善此瓶頸，通常會使用 最小堆（min-heap） 或其他平衡樹結構來維護「目前負載最小的機器」。在 min-heap 中，插入與取出最小值皆為 O(logm)，因此 n 個作業的分派成本為 O(nlogm)。

理論保證

問題設定

• 作業處理時間： [8,5,3,7,4,6]（單位時間）
• 機器數：m=3，機器記為 M₁,M₂,M₃
• 假設每台機器一次只能處理一個作業，作業不可中斷

LPT 前置步驟

• 排序（遞減）： [8,7,6,5,4,3]
• 資料結構：用 min-heap 維護「(目前負載, 機器編號)」，初始heap=[(0,M₁),(0,M₂),(0,M₃)].

逐步分派與負載更新

依序取出作業，將其指派給 目前負載最小 的機器，並更新該機器負載後放回 heap。每一步如下表（顯示「分派前的最小負載機器」與「更新後三台機器負載」）：

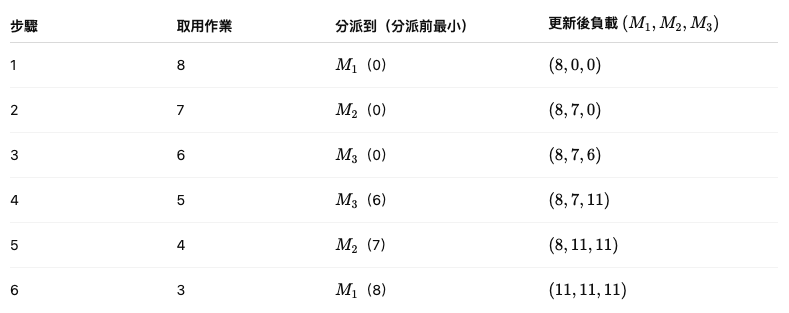
最終排程：
M₁ ：[0–8] 執行 8， [8–11] 執行 3 → 完工時間 11
M₂ ：[0–7] 執行 7， [7–11] 執行 4 → 完工時間 11
M₃ ：[0–6] 執行 6， [6–11] 執行 5 → 完工時間 11
最小完工時間 Makespan = 11。

下界驗證（最優解驗證） 計算兩個標準下界：

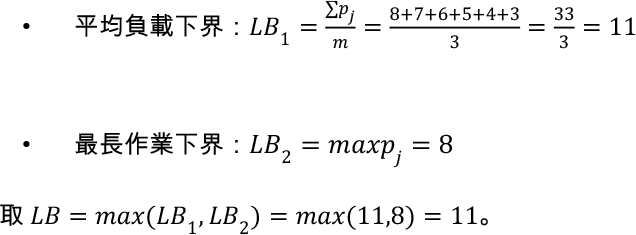
因為我們的排程達到下界 11，故必為最優。

延伸變體

雖然 LPT 演算法最初是為 同質平行機器（Identical Parallel Machines）的排程問題設計，但在不同情境下，人們對其進行了多種擴充與變體：

• 非同質機器（Heterogeneous Machines）
  當機器的處理速度不再一致，或每個作業在不同機器上有不同處理時間時，原始的「長作業優先」策略需要調整。研究者通常會將作業時間除以機器速度，或計算「標準化處理時間」，再依此排序與分派。這類情境的近似比率分析相對複雜，但概念仍延續 LPT「先考慮耗時較長的任務」的精神。
• 作業權重（Weighted Jobs）
  在部分問題中，每個作業除處理時間外，還伴隨「重要性」或「優先等級」。此時，目標可能從單純最小化 makespan 轉變為同時考量權重，例如最小化加權完工時間或同時控制最大負載。此情況下，需引入 Weighted LPT 或其他加權貪婪策略，使演算法能兼顧不同作業的相對價值。
• 即時排程（Online Scheduling）
  當系統無法預先得知所有作業，而是作業在運行過程中陸續到達（例如即時伺服器請求），可將 LPT 改為「到達即排序、即分派」的形式，並維持機器負載的即時最小化。這種線上版本雖無法完全比擬離線最優解，但在反應速度與資源利用率之間能取得平衡，適合高頻率請求環境。
• 多目標或限制式排程
  在實務上，排程往往伴隨額外約束，如任務必須遵守先後順序、部分作業不可在同一機器執行、或存在能源消耗與成本考量。LPT 可作為基礎，再加入限制檢查或啟發式調整，使其適用於更廣泛的情境。

應用場景

LPT 與其相關概念不僅存在於理論研究，更在多種工業與資訊領域中發揮重要作用：

• 雲端計算與資料中心
  當代資料中心通常需要在數以千計的伺服器間分配虛擬機（VM）或容器。透過類似 LPT 的策略，可以快速挑選負載最低的伺服器，將新的工作負載指派給它，確保系統在高併發下仍維持穩定的回應時間與均衡的資源使用率。
• 高效能運算（HPC）
  在科學模擬、人工智慧訓練等計算密集型任務中，常需同時使用大量 CPU/GPU 核心。利用 LPT，可在任務提交時，迅速將長任務優先排入閒置或低負載的核心，減少核心閒置，提升整體吞吐量。
• 製造與物流
  生產線作業通常由多個工序組成，若分派不當，最長的工序可能拖延整條產線的完工時間。LPT 的概念可協助工廠將「耗時較長的工序」盡早安插到可用的機台，縮短生產週期並避免瓶頸形成。在物流場景，例如包裝與配送中心，也能透過類似原則分配包裹處理任務。

Makespan Minimization 問題提供了一個分析「如何在有限資源中最有效率地排程」的基本框架，對理論與實務都具有深遠影響。儘管其屬於 NP-hard 問題，LPT 演算法 透過簡潔的「長作業優先」策略，在理論上具備不錯的近似比率，並在多種應用中展現良好效能。 在今日資料驅動與資源密集的運算環境中，理解這些基礎排程模型與演算法，能為設計更高效、可擴展的系統奠定穩固基礎。

參考資料：Graham, R. L. (1969). Bounds for certain multiprocessing anomalies. Bell System Technical Journal, 45(9), 1563–1581.