研究所考試
在電腦科學的理論中,「歸約(Reduction)」是一個極為重要的概念。簡單來說,歸約是一種將一個問題轉換成另一個問題的方式,使得若後者能有效解決,前者也能被間接解決。透過歸約,我們可以比較不同問題之間的計算困難度(computational complexity)。
特別是在 NP 完全(NP-complete)問題 的領域中,歸約扮演核心角色。若我們能將某一個已知的 NP 完全問題 A 在多項式時間內轉換成另一個問題 B,那麼 B 至少與 A 一樣困難。換言之,若 B 能在多項式時間內被解決,那所有 NP 問題也能被有效解決。這就是為什麼證明一個問題是 NP 完全時,通常需要兩個步驟:(1)證明該問題屬於 NP(可在多項式時間內驗證解答)。(2)找出一個已知的 NP 完全問題,並在多項式時間內將它歸約到此問題。
值得注意的是,不同問題之間的歸約方式各不相同,有些僅需簡單轉換輸入結構,有些則需要精心設計的數值編碼與邏輯對應。特別是將經典的 Vertex Cover(頂點覆蓋問題)歸約到 Subset Sum(子集合和問題)的過程,便是一個極具創意與啟發性的例子。
Vertex Cover 是圖論中的經典問題,也是 NP 完全理論發展早期的重要範例。


為了證明 Subset Sum 是 NP-Complete 的,我們需要從一個已知的 NP-Complete 問題出發,而 Vertex Cover 就是一個常見的選擇。其核心想法為:將「頂點是否選入 cover」編碼成數字,再用數字加總的方式模擬「每條邊是否被覆蓋」。
方法描述假設圖 G 有 n 個頂點與 E 條邊。我們為每個頂點與邊建立對應的數字,並使用 base-4(四進位) 來編碼。每個數字共有 E+1 個位元:其中最左位用來表示該元素是否為頂點,若為頂點則最左位為1,若為邊的補償變數(slack values)則最左位為0。右邊的 E 位用來表示各條邊是否被覆蓋(1 為覆蓋,0 為未覆蓋)。假設有一張圖共有三個頂點 {v1,v2,v3},其中 v1 與 v2 間有邊 e1,v2 與 v3 間有邊 e2。則總共會有五組編碼,分別如下所示:
| 元素 | e1是否覆蓋 | e2是否覆蓋 | base-4編碼 | 十進位 |
| v1(頂點) | 1 | 0 | 110 | 20 |
| v2(頂點) | 1 | 1 | 111 | 21 |
| v3(頂點) | 0 | 1 | 101 | 17 |
| y1(補償e1) | 1 | 0 | 010 | 4 |
| y2(補償e2) | 0 | 1 | 001 | 1 |
因著base-4是4進制,因此110轉換為十進位計算方式為1×42+1×41+0×40=20。
接著,我們設定目標數字 t 的結構為:t=[k,2,2,2,…,2]4,這個設定的意義為:左位的「k」代表我們要選取 k 個頂點;每條邊位上的「2」代表邊被覆蓋一次(頂點貢獻 1)並加上對應的 slack 變數(再貢獻 1),形成「2」。 若圖中有 E 條邊,則此數共有 E+1 位。
以範例來說,選擇 v2 即可覆蓋所有的邊,因此可以選 k=1,得到 t=[1,2,2]4。將其轉換為十進位是26,代表著若我們可以找到 subset sum 為26的子集合,就代表 k=1 時能找到1個頂點成為 vertex cover。子集合 {1,4,21} 可以滿足總和為26,其代表的意義為,扣除掉補償變數的剩餘編碼就代表構成 vertex cover 的頂點,也就是 v2。另一種選擇為 k=2,此時 t=[2,2,2]4,十進位是42。我們可以找到子集合 {1,4,17,20}、{1,20,21} 以及 {4,17,21} 都能滿足總和為42,而他們分別對應的 vertex cover 為 {v1,v3}、{v1,v2} 以及 {v2,v3}。
在理解如何將 Vertex Cover 歸約為 Subset Sum 的方法後,我們來看歷屆試題是怎麼考的,台大資工在110年資料結構與演算法最後一題就考了這個觀念:
前置作業(建構base-4編碼)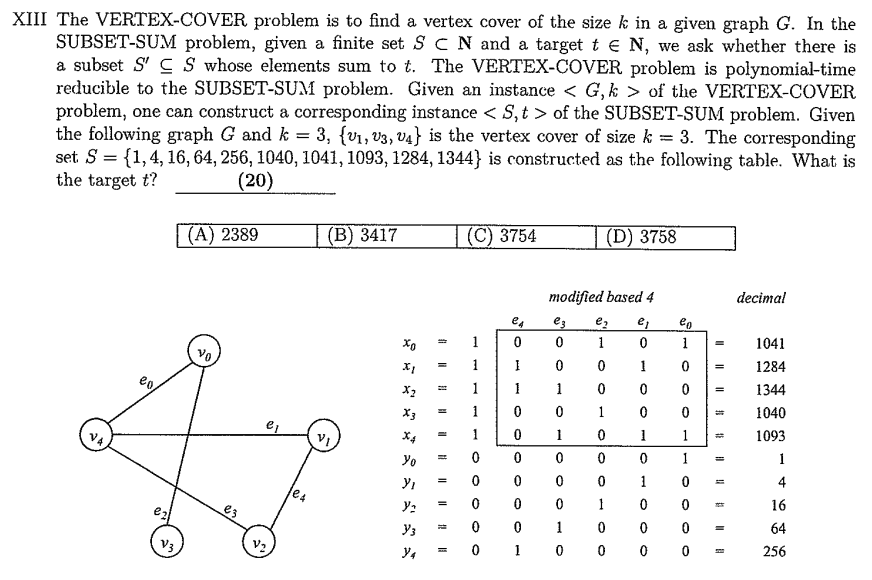
這題很好心的幫我們把前置作業都寫好了,前面有看懂歸約方法的同學們應該早就把 t 是多少給解完了吧!所以我們改一下題目,假裝我們只知道 k=3,然後要透過 subset sum 的計算方式來得到 vertex cover 有哪些頂點!首先建構每個頂點的base-4編碼,頂點的最左位是1,接下來五位則是看是否覆蓋 e4 至 e0 這五個邊,若覆蓋填1,沒有則填0。題目中的 x0 代表 v0 的變數,邊 e0,e2 被該頂點覆蓋,因此編碼為:100101,十進位為1041,變數 x1 至 x4 用相同方法即可計算出對應base-4編碼。接下來我們要計算每個邊對應的補償變數(slack values) y0,y1,…,y5,他們計算的方式相對簡單,最左位固定為0,而剩餘位除了自己代表的邊為1以外,其他皆為0,例如 y0 對應的base-4編碼為:000001。
建構目標 t題目指定 k=3,所以我們知道 t 的第一位是3。接下來會有 E 位都是 2,因此 t=[3,2,2,2,2,2]4,換算成十進位:t=3×45+2(44+43+42+41+40)=3754,即為本題答案。
尋找對應子集合根據前面計算的base-4編碼換算成十進制,可得整個集合:S={1,4,16,64,256,1040,1041,1093,1284,1344}。而目標值 t=3754,代表我們要在集合 S 當中找到總和為3754的子集合。我們先找出三個頂點 v1,v3 和 v4 ,他們可以覆蓋所有的邊,為其中一組可行的 k=3 的 vertex cover,對應的變數 x1,x3 和 x4,將他們的base-4編碼加總為:1284+1040+1093=3417。接著觀察哪些邊僅被覆蓋一次,我們需要補上對應的補償變數,例如 e0 僅由 v4 覆蓋,因此需要補上補償變數 y0。而 e1 同時由 v1 和 v4 覆蓋,因此就不需要補上對應的補償變數 y1。最後需要補上的補償變數為 y0,y2,y3,y4,將他們的base-4編碼加總為:1+16+64+256=337。將此數值與前面的總和3417加總,可得3754,與目標值 t 相等。因為找到子集合的總和符合目標值,代表 subset sum 問題有解,同時也代表對應的 vertex cover 問題有解,其對應的 vertex cover 為 {v1,v3,v4}。
歸約不僅是理論上的工具,也是一種理解問題本質的橋樑。在這個例子中,我們從 Vertex Cover 出發,透過數位化的思考與base-4編碼,精確地將圖形覆蓋的問題轉化為子集合和的問題。這證明 Subset Sum 至少與 Vertex Cover 一樣困難,也因此屬於 NP 完全問題。雖然 Vertex Cover 是圖論問題,而 Subset Sum 是數值問題,但兩者本質上都要求一種「組合式選擇」:Vertex Cover 要求選哪些頂點覆蓋所有邊;Subset Sum 要求選哪些數字讓加總達成目標。透過編碼(encoding),我們用數字的「每個位元」模擬圖中「邊的狀態」,讓覆蓋的概念轉化為數值相加的概念。這種思維方式是 NP 完全理論中最具啟發性的部分,揭示了計算問題間的「可轉換性」與「共通困難」。

