研究所考試
上回說到,在演算法領域中,許多實務上經常遇到的問題屬於 NP-complete 或 NP-hard 類別,代表目前尚無已知能在多項式時間內找到最佳解的方法。儘管這些問題在理論上困難重重,現實中卻無法迴避,因此需要採取替代策略來解決他們。其中,近似演算法(Approximation Algorithms)是一種常見且實用的方法,目標是在合理的時間內產生接近最佳的可行解。我們也介紹了近似比率(approximation ratio)的概念,它用來衡量近似解的表現有多好,代表近似解與最佳解之間的差距。如果設計出的近似演算法,其近似解與最佳解的關係能達到某個近似比率(假設為α),則該近似演算法可以被稱作α-approximation algorithm。對於最小化問題,近似解通常大於最佳解,而最大化問題則相反。近似比率的數值永遠不小於 1,越接近 1 表示解越好。這些演算法常常在計算時間與解的精確度之間取得權衡,特別適合應用在資源有限或需要即時處理的情境中。
我們以頂點覆蓋問題(The vertex cover problem)這個經典的最小化問題作為範例,演示了該問題的近似演算法設計方式。該近似演算法的近似比率為2,也就是說透過該方法得到的近似解,裡面的頂點數量不會超過最佳解的2倍。且該近似演算法的時間複雜度為O(V+E),能在多項式時間內執行完成,比最佳解還快上不少。這次,我們要繼續探討其他經典問題的近似演算法,希望讀者能在閱讀完後更加了解近似演算法。
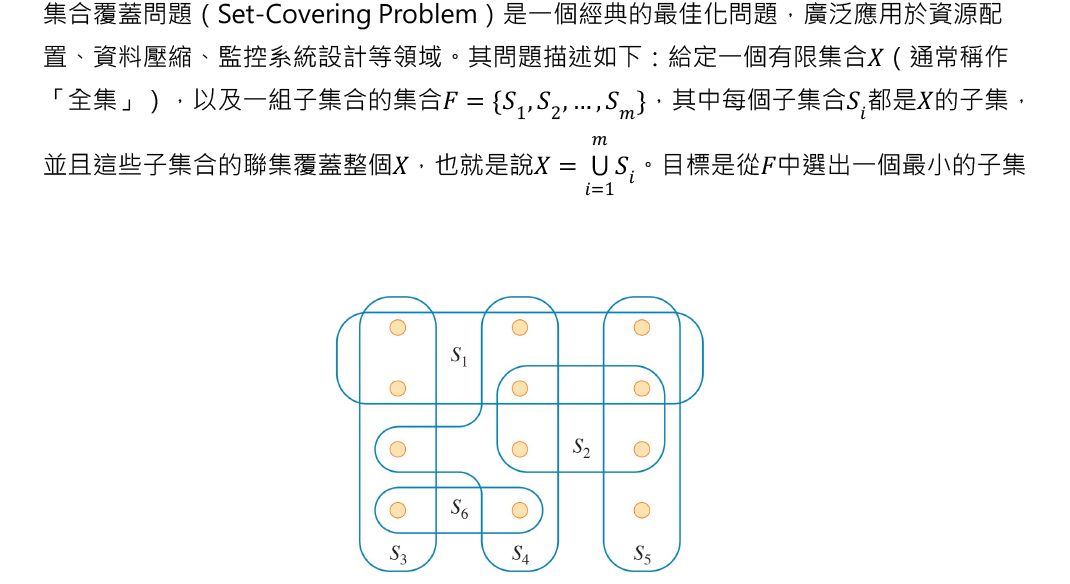

集合覆蓋問題可以用來描述很多問題情境,例如我們假設X代表完成某項任務所需要的一系列技能。公司裡的每一位員工都會擁有所需技能裡的一部分,全公司加在一起一定可以完成這項任務。但站在成本考量上,我們會希望參與這項任務的人力越少越好,最終目標為希望用最少的人力,讓完成這項任務所需要的一系列技能至少都有一個人會。集合覆蓋問題已被證明為 NP-hard 問題,因此一般情況下難以在多項式時間內求得最佳解,實務上常透過近似演算法來節省時間,並取得可接受的解。
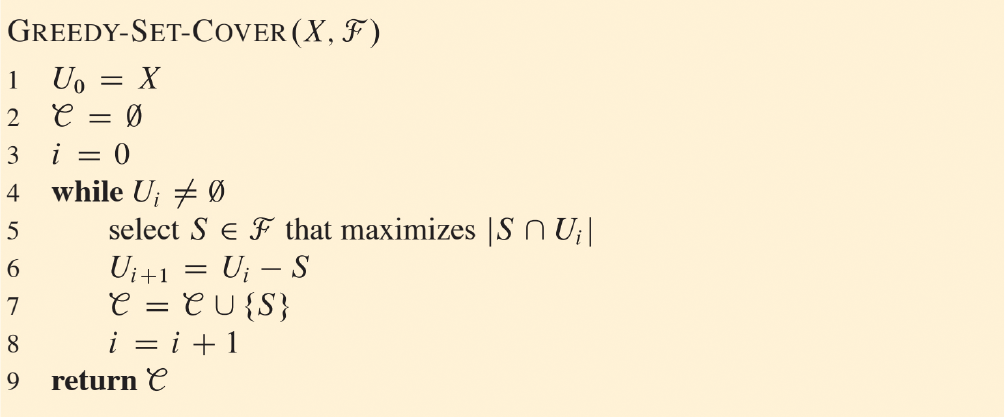
這邊要介紹的是透過貪婪法(Greedy Method)設計的近似演算法,一般稱作貪婪近似演算法(Greedy Approximation Algorithm)。此方法的設計概念很簡單,在每一個階段都挑選子集合Si,該子集合可以覆蓋最多還沒有被覆蓋的元素。如果以上面的圖當作例子的話,第一個被挑選到的子集合為S1,因為它可以一次覆蓋6個還沒有被覆蓋的元素。接著被挑選的是子集合S4,它可以一次覆蓋3個還沒有被覆蓋的元素。下一個被挑選的是子集合S5,它可以一次覆蓋2個還沒有被覆蓋的元素。最後輪到子集合S3或子集合S6,選擇任意一個都可以覆蓋最後一個還沒有被覆蓋的元素。換成公司的例子會更好理解這個演算法的操作方式,在挑選第一個員工時,會選擇具有最多技能的那位。接下來每一次挑選人選時,都會找具有最多還沒有被滿足的技能的員工加入集合X。
在理解設計概念後,接著我們來看寫成演算法會怎麼運作吧!
這個方法是這樣運作的:在每次進入while迴圈時,Ui代表的是還沒有被覆蓋的元素集合,最一開始的時候全部元素都還沒有被覆蓋,因此U0=X。集合C搜集了所有被選中的子集合,例如{S1,S4,S5,S3}。第5行就是貪婪法運用的地方,會挑選能覆蓋最多還沒有被覆蓋的元素的子集合S。第6行會把Ui更新,扣掉那些被S覆蓋的元素,而第7行會把S加入到集合C當中。當Ui=Ø時,就代表所有元素都被覆蓋,演算法在此終止。
此貪婪近似演算法求得的近似解,其近似比率為O(lgX),也就是説此演算法為O(lgX)-approximation algorithm。詳細分析剛好近幾年有考過,我們就接著看歷屆試題吧!
- 實戰演練:111成大資訊聯招碩士班「程式設計」考題



