研究所考試

在演算法的經典問題裡面，有一個相當大的問題分支，叫做圖論（Graph Theory）。當我們在探討圖論時，核心目標是理解節點（vertex）與邊（edge）之間的關係與結構。圖可分為無向圖（undirected graph）與有向圖（directed graph），其中有向圖中的邊具有方向性，常用於描述單向的關係，例如網頁連結和流程控制。

在圖的分析中，一個重要的性質是「可達性」：若存在從節點 u 到節點 v 的路徑，我們稱 v 可由 u 到達。在無向圖中，若任意兩節點皆可互相到達，則該圖是連通的（connected）。對於有向圖，這一性質進一步擴展為強連通性（strong connectivity）。一張有向圖中，若某個節點集合 C⊆V 滿足：對任意 u,v∈C，皆存在從 u 到 v 及從 v 到 u 的有向路徑，則 C 稱為一個強連通單元（Strongly Connected Component, SCC）。整張圖可能會由多個不相交的 SCC 所組成。尋找 SCC 是分析圖結構、縮減複雜度、甚至進行高階邏輯推論（如 2-SAT 問題）的基礎。

強連通單元的應用廣泛出現在資訊工程中。例如，在網頁排名演算法（如 PageRank）中，強連通的網頁群組可能代表主題一致或互相推薦的網站群；在程式靜態分析中，強連通單元能協助辨認循環依賴模組與控制流中的迴圈結構；在社群網路分析中，強連通群組可能代表緊密互動的使用者社群。透過強連通單元的辨識，我們能有效將複雜系統簡化成有意義的子結構。這次，我們要繼續探討其他經典問題的近似演算法，希望讀者能在閱讀完後更加了解近似演算法。以下我們將詳細介紹強連通單元的定義，以及在圖形中尋找強連通單元的演算法該如何運作，希望讀者能在閱讀完後更加了解這個問題的解法。

問題描述

在一張有向圖 G=(V,E) 中，存在最大頂點集合 C⊆V ，滿足 C 中任意兩頂點 u,v 皆相互連通，也就是皆存在從 u 到 v 及從 v 到 u 的有向路徑，則 C 稱為一個強連通單元（Strongly Connected Component, SCC）。

圖例

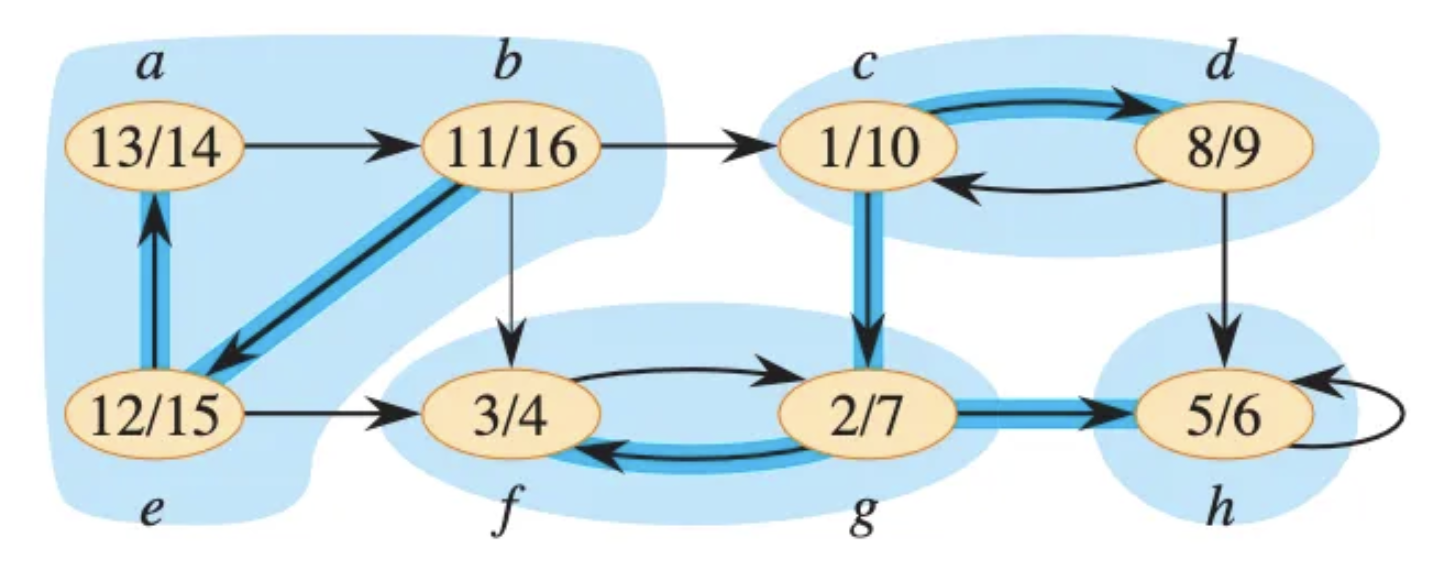
這張圖展示了一張有向圖中各個強連通單元的分佈情形。每個被淡藍色區塊圈起來的區域，代表一個強連通單元，也就是圖中節點彼此之間皆可互相到達的最大集合。舉例來說，點集合 {a, b, e} 為一個強連通單元，因為他們三個形成一個迴圈，互相都可以到達彼此，然而若想要加入任意相鄰頂點，例如 c 或 f，則會發現皆無法達成互相連通的條件。此外，每個橢圓形節點中的兩個數字分別代表該節點在深度優先搜尋（DFS）過程中的發現時間和完成時間，這也反映出演算法在找出強連通單元過程中對節點的探索順序。在開始講解尋找強連通單元的演算法之前，我們先來幫各位複習一下深度優先搜尋（DFS）是如何運作的。

介紹

深度優先追蹤（DFS）是一種遍歷圖的方法，其基本策略是「儘可能深入探索圖的分支」，直到無法繼續為止再回溯。DFS 是多種圖論演算法的基礎，包含拓撲排序、找出連通元件、檢測環、以及本文的重點——強連通單元。

深度優先追蹤的操作流程 給定一張有向圖 G=(V,E)：
（一）為所有節點初始化狀態為「未訪問」。
（二）對每個未訪問的節點 u，執行遞迴：

1. 將 u 標記為訪問中。
2. 遍歷所有從 u 出發的鄰接節點 v，對尚未訪問的 v 執行深度優先追蹤。
3. 當所有子節點回溯完畢後，將 u 標記為「已完成」並記錄其完成時間。

其中每個節點會有兩個時間戳：
（一）發現時間 d[u]：首次拜訪節點 u 的時間戳。
（二）完成時間 f[u]：節點 u 完成所有後代探索的時間戳。

預備 G 的反向圖 G^T

定義 G^T=(V,E^T)，將原圖中每一條有向邊 (u, v) 替換為 (v, u)，也就是反轉所有邊的方向。此舉會保留圖中所有節點的連結性資訊，但改變了每個節點的出入邊關係。

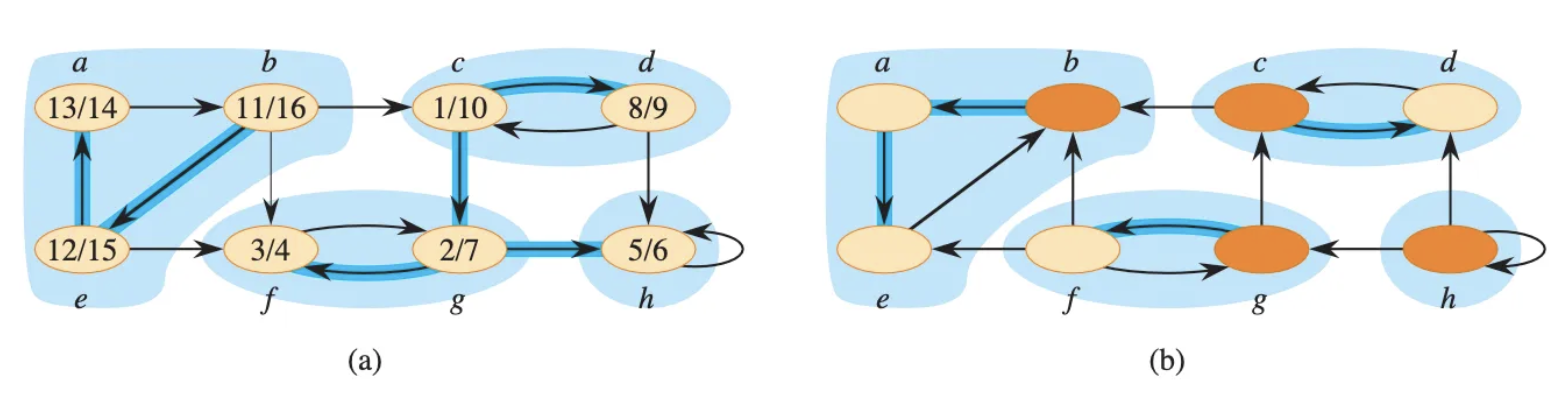
值得一提的是，原圖 G 的強連通單元和轉置圖 G^T的強連通單元是一樣的。讀者可以在反向後的圖形上，利用前面提到的定義驗證正確性。

演算法介紹步驟說明：

（一）第一次 DFS：記錄完成時間。會先對原圖 G=(V,E) 執行一次深度優先追蹤。每當某個節點完成探索時，可選擇將其 push 進一個堆疊（stack）或記錄其完成時間（依據不同實作方式有不同選擇）。

（二）建立反向圖 G^T：對原圖的每一條邊 (u,v)∈E，在反向圖中建立邊 (v,u)。

（三）第二次 DFS：依照完成時間反向順序。對反向圖 G^T=(V,E^T) 執行一次深度優先追蹤。拜訪節點的順序依照第一步中完成時間反向順序進行。每一次新的 DFS 遍歷所接觸到的一整群節點，即構成一個強連通單元。

演算法實作

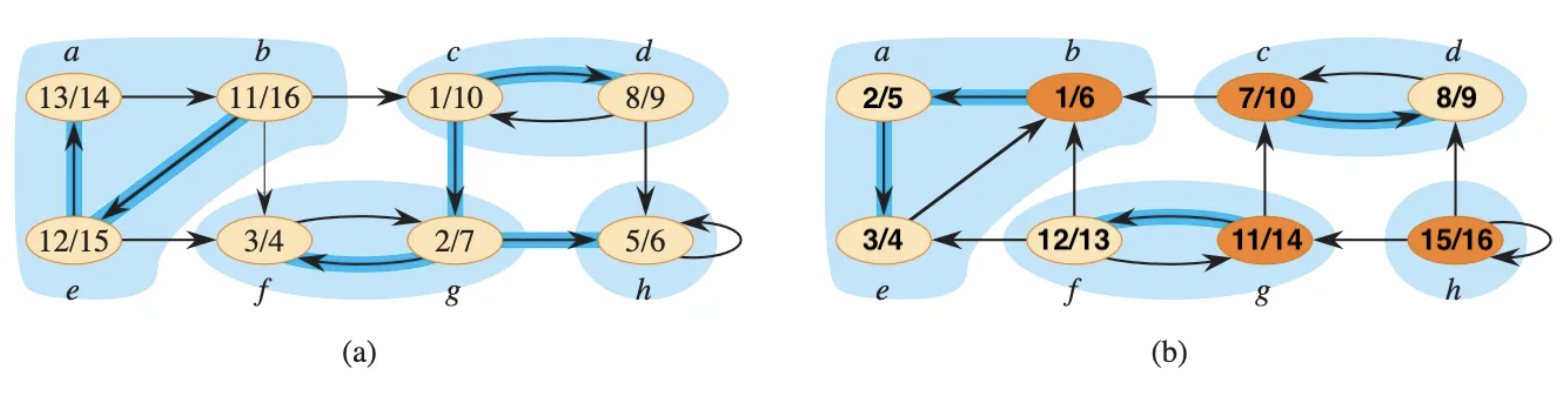
左邊的圖是經過第一次的深度優先追蹤後，每個節點會有各自的發現時間以及完成時間兩個時間戳。接著對每一條邊 (u,v)∈E，在反向圖中建立邊 (v,u)。建立完成後，對右邊的反向圖再進行一次深度優先追蹤，順序是按照前面的完成時間反向進行。換句話說，左邊那張圖的節點中，右邊數字（完成時間）越大的節點，在第二次深度優先追蹤就會越早被探尋到。例如節點b在左邊圖形裡的完成時間是16，是所有節點裡最晚的，因此在右邊圖形裡，節點b的左邊數字（開始時間）是1，是所有節點裡最早被探尋的。經歷過兩次深度優先搜尋後，在反向圖中找到的深度優先追蹤森林（DFS Forest），就是原圖的強連通單元。

除了搜尋演算法與理論應用，SCC 的概念也廣泛出現在現代大型系統架構設計中。例如在微服務系統（microservice architecture）中，每個服務可能都有依賴其他服務的關係圖。若存在一個強連通單元，代表這些模組間具有相互依賴關係，容易形成耦合過高的結構，會影響系統的可維護性與測試效率。

此外，在資料流分析（Data Flow Analysis）與硬體電路設計中，SCC 可協助識別訊號循環與同步單元。在 AI 領域的神經網路圖中，若某些節點形成 SCC，可能代表循環神經網路（RNN）或圖神經網路（GNN）的特定模組。這些應用顯示 SCC 不只是理論工具，也具有高度的工程實用價值。

強連通單元是圖論中一個好玩又實用的概念，透過深度優先搜尋與圖的轉置操作，Kosaraju’s Algorithm 能在不增加時間複雜度的情況下，準確識別圖中的所有 SCC。掌握這一演算法的過程，有助於讀者進一步理解圖的分解、資訊流向，以及更複雜的應用場景！