研究所考試
在大學的演算法課程中,會學習利用貪婪法、分治法、動態程式規劃等觀念來設計方法,並正確的解決眼前遇到的問題,例如最短路徑、排序、搜尋...等。然而在現實世界中,許多問題的求解不僅需要正確性,還必須考慮效率。對於某些計算複雜的問題,尋找最優解往往需耗費大量時間與資源,甚至在理論上也無法在合理時間內完成。舉例來說,如果希望導航計算出從台北車站到墾丁的最短距離,卻需要花費半小時才能計算出真正最短的路徑,相信沒有人會願意等待這麼久的時間。
為此,演算法學者提出了「近似演算法」(Approximation Algorithms)作為一種可行的解法策略。近似演算法不保證能找出絕對最優解,但能在合理時間內產生接近最優的解,並提供解的品質保證。用上面舉的例子來說,或許找到的並非從台北車站到墾丁的絕對最短距離,但使用的演算法僅需要5秒便可執行完成,且獲得的路徑距離也算短,那使用近似演算法來解決此問題就會更為合理。通常來說,近似演算法被廣泛應用於圖論、最佳化、資源分配等領域,特別適合用於處理比較難的問題(NP-hard)。透過近似演算法,我們能在可接受的誤差範圍內,取得實用且高效率的解決方案,是結合理論與實務需求的重要工具。本文將以目前最常使用的演算法經典教材《Introduction to Algorithms》為基礎,介紹其中對於近似演算法的定義,並透過範例讓同學們能順利上手。
在演算法領域中,許多實用且重要的問題屬於 NP-complete 或 NP-hard 類別。這代表目前尚無已知的方法能在多項式時間內找出其最佳解(optimal solution)。儘管如此,這些問題在現實世界中依然頻繁出現,無法因為其困難性而忽略不處理。因此,演算法設計者們提出了幾種策略,嘗試在合理時間內對這些「計算上非常困難」的問題給出實用的解法:
第一種策略是觀察實際應用中的輸入規模。如果問題的輸入規模不大,即使使用指數時間的演算法,也有機會在短時間內完成運算並找出正確答案。
第二種方式是針對特定情境或常見的實例進行優化,將其從整體問題中獨立出來,藉此設計出能在多項式時間內解決的特例演算法。
第三種,也是最具廣泛應用性的方法,則是退而求其次:設計能在多項式時間內求出「接近最優」解的演算法,也就是近似演算法(approximation algorithms)。
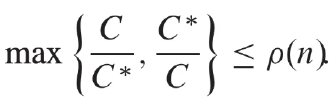
最佳化問題是一類目標明確的計算問題,目的是在所有可行解中找出最「好」的解。這個「好」的標準可能是最大化(如利潤、效率)或最小化(如成本、時間)。當我們使用近似演算法來解決最佳化問題時,如果是最大化問題,近似演算法得到的解就會略小一點;反過來說,如果是最小化問題,近似演算法得到的解就會略大一點。既然近似解跟最佳解之間存在差距,就會需要一個標準來衡量近似解的表現如何,這個指標被定義為近似比率(approximation ratio, ρ(n))。
定義 C 為近似演算法的解答,C* 為最佳解,則兩者與近似比率具有以下關係:如果設計出的近似演算法,其近似解與最佳解的關係能達到某個近似比率(假設為α),則該近似演算法可以被稱作 α-approximation algorithm。舉例來說,如果我們針對前面提到的最短路徑設計近似演算法,並且能確保近似解的距離最差會是最佳解的 1.2 倍,那就可以說這個近似演算法是 1.2-approximation algorithm。
對於最大化問題,因為最佳解 C*會比近似解 C 還要大 (0 < C ≤ C*),根據計算近似比率的公式,可得近似比率會是 C*/C。與之相對的,對於最小化問題,因為最佳解 C*會比近似解 C 還要小 (0 < C* ≤ C),根據計算近似比率的公式,可得近似比率會是 C/C*。綜合以上兩種情況,可以知道在《Introduction to Algorithms》這本書的定義裡,近似比率永遠不會小於1,因為當 C/C*≤1 時,C*/C≥1。若一個演算法的近似比率為 1(稱為 1-approximation algorithm),則它所產生的解即為該問題的最佳解。
值得一提的是,近似演算法在實作上經常涉及一項效率與精確度的權衡(trade-off)。一般而言,計算時間越長,越有可能取得接近最佳解的結果,也就是近似比率越趨近於 1。然而在資源有限或時間受限的情況下,適當的近似解往往比費時計算的最佳解更為實用。
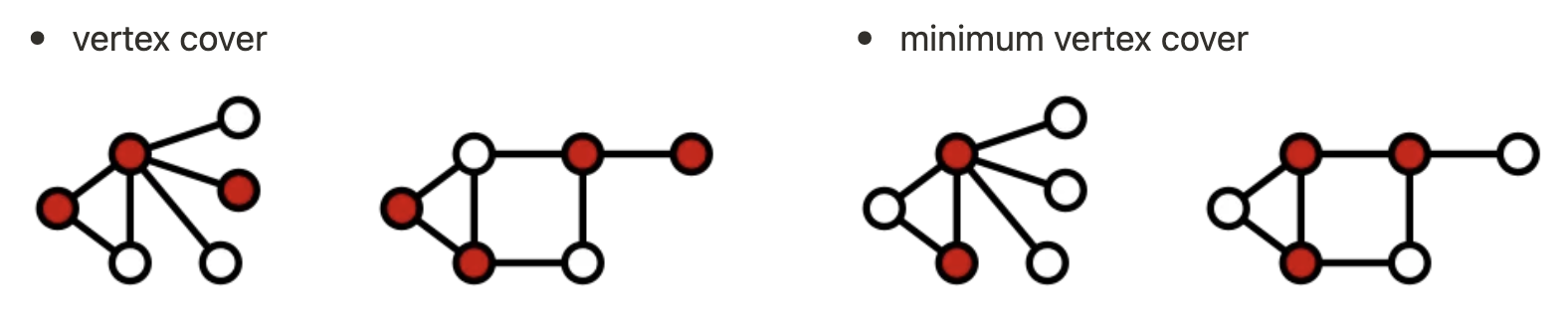
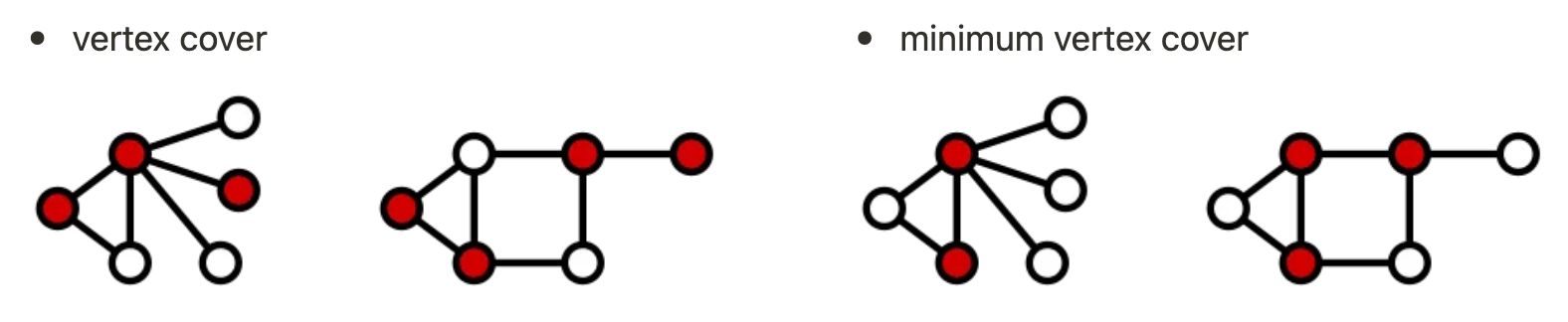
頂點覆蓋問題是一個圖論中的經典問題,其目標是在一張無向圖中,選出一組頂點,使得每一條邊至少有一端連接到這些選出的頂點,並且希望這組頂點的數量最少。這裡要特別強調的是「數量最少」這四個字,也就代表說如果找出來的頂點集合符合「每一條邊至少有一端連接到這些選出的頂點」,但卻能找到更小的頂點集合,就代表這個解並非最佳解。舉例來說,下圖的左側紅點只能稱為頂點覆蓋(vertex cover),右側紅點則是最小的頂點覆蓋(minimum vertex cover),而右側的紅點才符合頂點覆蓋問題的最佳解。

首先將原本圖形中的邊 E 複製一份儲存到邊集合 E’中。當邊集合 E’不是空集合時,在其中挑選任意邊 (u,v),將兩側頂點都加入點集合 C 中,並將與 u,v 相鄰的所有邊從 E’中刪除。不斷重複以上步驟直到邊集合 E’成為空集合,點集合 C 就是頂點覆蓋問題的近似解。
透過以上方法所取得的點集合 C 是頂點覆蓋問題的近似解,而其近似比率為 2。換句話說,以上方法為頂點覆蓋問題的 2-approximation algorithm,也就是說透過該方法得到的點集合 C,裡面的頂點數量不會超過最佳解的 2 倍。如果利用鄰接串列(adjacency list)來表示圖形的話,該近似演算法的時間複雜度為 O(V+E),能在多項式時間內執行完成,會比原本的最佳解還要快上許多。然而,近似演算法要成立,還需要檢查兩件事情,分別是正確性和近似比率:
- 正確性:解出來的點集合 C 是頂點覆蓋
首先,所有被加入 C 的頂點,跟他相鄰的邊都會被移除。同時演算法的終止條件為,所有的邊都從邊集合 E’被移除。綜合以上兩點,可以得知所有的邊都至少有其中一邊的頂點是在點集合 C 裡面的,因此符合頂點覆蓋的定義,確保該近似解的正確性無誤。 - 近似比率
假設集合 A 是在上面演算法中第 4 行被選到的邊集合,要能夠去覆蓋 A 裡面的所有邊,就代表 A 裡面的所有邊,都至少有一側頂點屬於頂點覆蓋。那因為集合 A 的邊被選中時,會將與其兩側頂點相鄰的所有邊都移除,因此集合 A 裡面的所有邊兩側頂點都不相同。換句話說,在 A 中任意邊的兩側頂點,都不可能被同一個頂點覆蓋裡的頂點給覆蓋(意思就是兩側頂點都會出現在任意頂點覆蓋中,|C*|≥|A|)。那剛才有提到,在 A 裡面的所有邊,兩側頂點都不重複,也就是說最後得到的點集合 C,裡面的頂點數量為 2|A|。最後整理數學式,可得 |C|=2|A|≤2|C*|,因此可知近似比率 C/C*≤2,確保該方法為 2-approximation algorithm。

