首頁資訊考點新歷期

研究所考試

演算法常考題：差分約束與最短路徑
發佈時間：20250408

演算法（Algorithm）是資工所的重點科目之一，同時也是成為工程師的必備技能。演算法關注如何以有效率、可行且有邏輯的方式，處理各種運算任務，例如排序、搜尋、圖論問題、數值計算等。其中不乏很多核心概念，例如貪婪法、分治法、動態規劃，工程師往往會以這些方法作為出發點，開發新的演算法以符合需求。良好的演算法設計能大幅提升程式效能，是程式開發與工程應用不可或缺的基礎。本文將以目前最常使用的演算法經典教材《Introduction to Algorithms》為基礎，介紹考試中常見的演算法觀念與解法。

差分約束與最短路徑

差分約束與最短路徑是很經典的演算法考題，近十年來在研究所考卷裡出現無數次，足以說明這個問題在出題老師心中的地位。這個問題很有趣的地方在於，乍看之下會是一連串的不等式，長得一臉像是數學問題，然而實際上卻要用到圖論的觀念來解題！

舉例來說，看到的題目會長這樣：

x1-x2 ≤0,
x1-x5 ≤-1,
x2-x5 ≤1,
x3-x1 ≤5,
x4-x1 ≤4,
x4-x3 ≤-1,
x5-x3 ≤-3,
x5-x4 ≤-3.

然而到了實際解題時，題目會變成這樣：
中間究竟是變了什麼魔法？就讓我們看下去吧！

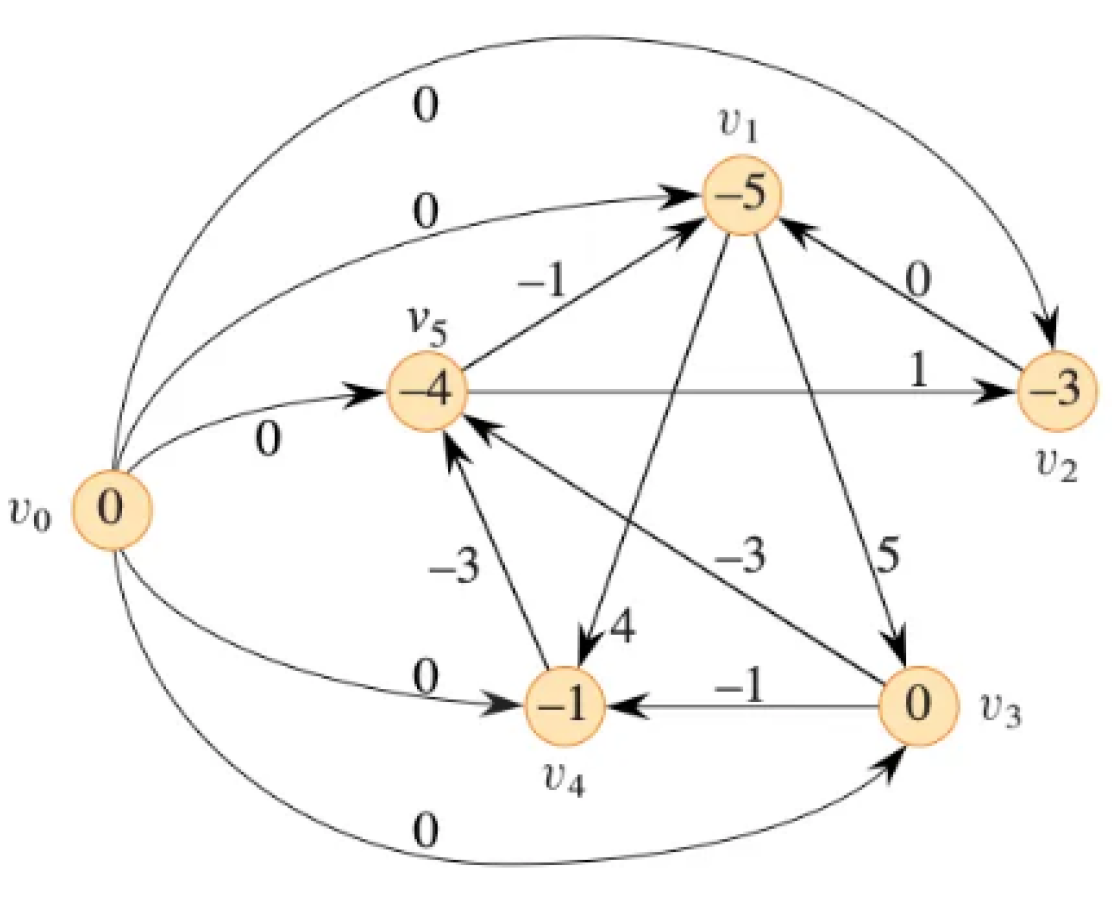
觀念與解題思路
差分約束系統
題目有時候會直接給很多組不等式，也可以包裝在許多應用中，例如排程、時序分析、資源配置等。不過無論如何，我們可以整理出多組形如以下的不等式限制：

xi-xj≤c

這種限制表示變數xj相對於xi的最大差距不能超過常數c，這樣的不等式系統稱為差分約束系統（Difference Constraints System）。
和圖論的關係
每一條不等式xj-xi≤c可以轉換為一條有向邊，遵守以下規則：
  1. 這個有向邊從節點i指向節點j
  2. 邊的權重為c
舉例來說，假設不等式為x1-x2≤0，透過上述規則可轉換：
  1. 這個有向邊從節點2指向節點1
  2. 邊的權重為0
這就是為什麼在上面的圖中，有一條權重為0的有向邊從v2指向v1。

如此一來，整個差分約束系統就可以視為一張帶有權重的有向圖。
求解是否存在滿足所有不等式的變數值，就等同於在這張圖上進行最短路徑分析。

解題步驟
  1. 建立有向圖
    • 根據題目條件的不等式，轉換出對應有向邊。
  2. 加入虛擬節點v0
    • 新增一個虛擬節點v0。
    • 對每個節點vi加入一條從v0到vi的邊，權重為0。
  3. 以虛擬節點為起點，執行最短路徑演算法（Bellman-Ford）
    • 如果圖中不存在負迴圈（negative cycle），則此問題有解。
    • 反之，則代表存在邏輯衝突，無解。
實戰演練：113成大資工所「資料結構及演算法」考題
15. (10%) Find the set of feasible solutions {x = (x1, x2, x3, x4, x5)} or determine that no feasible solution exists for the following system of difference constraints:
x1 - x3 ≤ 1
x2 - x3 ≤ 4
x4 - x5 ≤ -2
x3 - x4 ≤ 4
x5 - x1 ≤ 3
x4 - x2 ≤ -7
x1 - x2 ≤ -2
x5 - x3 ≤ 1
解題思路
將不等式轉換為有向邊
  • x1-x3≤1：從節點3指向節點1的有向邊，權重為1。
  • x2-x3≤4：從節點3指向節點2的有向邊，權重為4。
  • x4-x5≤-2：從節點5指向節點4的有向邊，權重為-2。
其餘不等式以此類推，共轉換出8個有向邊。
加入虛擬節點
  • 新增一個虛擬節點v0。
  • 對每個節點vi加入一條從v0到vi的邊，權重為0。
共轉換出5個權重為0的有向邊。
執行最短路徑演算法（Bellman-Ford）
  • 以虛擬節點v0為起點，執行最短路徑演算法。
  • 虛擬節點v0到其他節點的最短路徑，就是這個問題的解。
經過計算可得x={1,3,0,-4,-2}為其中一組可行解（feasible solutions）。
延伸學習
  • 《資料結構重點整理》，王致强編著，高點文化出版。ch8圖形，8-6最短路徑問題。
  • Introduction to Algorithms by CORMEN p.626
 
關鍵詞
差分約束、最短路徑、圖論、Bellman-Ford
上一篇：從科技、金融、AI，談資工就業與考研趨勢
回首頁：資訊考點新
我要諮詢