【推薦書籍】
統計學(含概要)歷屆試題詳解、
統計學:重點觀念與題解(上) 、統計學:重點觀念與題解(下) 、計量經濟學與財務工程、
統計學精選666題
【推薦課程】
行動版、數位課程
篇名
過度擬合 (overfitting) 與正則化 (regularization)
作者
許誠哲
說明
發佈時間:20240520
若為了增加對於資料的預測能力, 使用較為複雜的模型(例如使用更多解釋變數或者引入三階以上的次方項), 雖然對於原先的資料相較於簡單的模型有較好的配適能力,但若對於新資料的配適能力比簡單的模型更差, 則稱此模型存在著過度擬合問題。若研究者可以接受犧牲一些樣本內的配適能力以交換樣本外的預測能力(或稱作預測的一般性),可採取正則化。正則化為在損失函數中加入

對於原資料的配適稱作樣本內 (in-sample) 預測, 對於新資料的預測稱作樣本外 (out-of-sample) 預測。如圖所示:
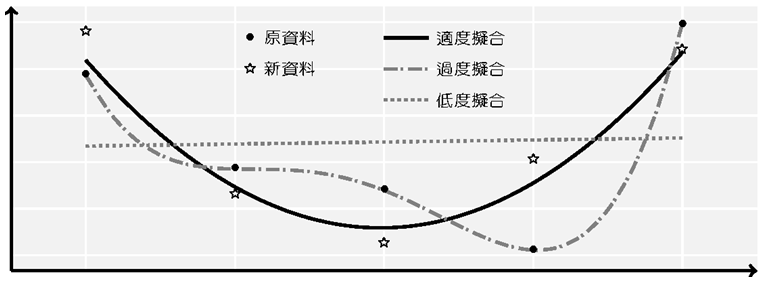
黑點為原先資料, 星號為新資料。黑實線為簡單的二次式模型, 灰虛點線為四次式模型, 灰點線為簡單迴歸模型。可看出灰虛點線雖然在樣本內完美的配適, 但樣本外配適能力較差, 因此四次式模型有過度擬合問題。但簡單迴歸模型樣本內與樣本外的配適能力都很差, 則稱此模型為低度擬合 (underfitting)。若使用機器學習方法進行大數據分析時, 使用過度複雜的模型雖然可以增加樣本內預測能力, 但可能損失對於樣本外的預測力。當收縮參數越大, 則對於使用參數的懲罰越強, 因此參數的最適值會越小或者為 0。若最適係數大部份為 0, 僅有少部份係數不為 0 的模型稱作稀疏化模型 (sparse model)。
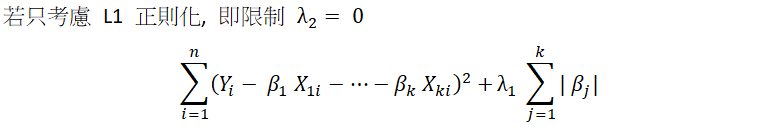

關鍵詞
過度擬合、正則化、收縮參數、迴歸模型
刊名
商研所許誠哲
該期刊-下一篇

