在大學的統計學課程中的迴歸分析， 大多對誤差項進行同質性(homoskedasticity) 假設。意即假設給定不同的 X， 則誤差項的變異數皆為常數， 其中誤差項即為樣本點偏離迴歸線的分散程度之衡量。舉例來說， 若 Y 為薪資， X 為教育程度， 則同質性隱含各種教育程度下， 薪資的分散程度皆相同， 但這個假設很明顯的並不合理。實際上的資料， 通常教育程度越高， 則薪資的分散程度越大。例如以之前專欄提過的薪資實價登錄平台的資料為例， 大學以下學歷的薪資標準差為 9017 元， 碩士學歷的薪資標準差為 12780 元， 而博士學歷的則為 17873 元。
在本次的專欄中， 我將討論異質變異數對於單一係數檢定的影響。為了方便分析， 我將模型設為最單純的簡單迴歸模型， 模型設定為

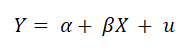
其中我將樣本數設定為 100， 母體截距設定為 2， 母體斜率設定為 0， 誤差項 u 則服從常態分配， 其平均數為 0， 變異數有不同的設定。由於變異數需為正， 因此我將 X 設定的母體分配為 Poisson 分配， 其平均為 15。 對於變異數的設定有同質變異數與異質變異數， 異質變異數又細成與 X 呈正比和與 X 呈反比， 如下所示：

1. 設定 1， 同質變異數： u 的標準差設定為 10
2. 設定 2， 異質變異數 1： u 的標準差設定為 10 X
3. 設定 3， 異質變異數 2： u 的標準差設定為 10/X

在設定的顯著水準為 0.05 下， 由於真實斜率為 0， 因此斜率的係數檢定統計量之絕對值若大於 1.96， 則可拒絕虛無假設。若模型為正確設定， 此時可拒絕虛無假設的機率應為設定的顯著水準 0.05。

在統計課程中學到的斜率係數標準誤的計算公式 (以  表示) 是建立在同質性假設下， 但在計量經濟的課程中學到的 HC 標準誤 (以  表示) 並未假設同質變異數， 因此在異質變異數下亦適用。

兩者的計算公式如下：

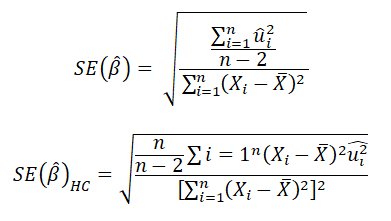
在此我分別對 3 種誤差項標準差的設定各進行 10000 次模擬， 每次模擬均分別使用兩種標準誤計算係數檢定統計量， 最後分別得到使用兩種係數標準誤下， 錯誤拒絕虛無假設的樣本比例作為比較。
程式碼如圖 1 所示。 模擬結果如下：

1. 設定 1： 使用一般標準誤 0.0490， 使用 HC 標準誤 0.0435
2. 設定 2： 使用一般標準誤 0.0788， 使用 HC 標準誤 0.0425
3. 設定 3： 使用一般標準誤 0.0917， 使用 HC 標準誤 0.0406

可以看出無論變異數的設定為何， 使用 HC 標準誤的顯著水準皆相當接近且並未高於 0.05。而使用一般標準誤下， 若誤差項真的具同質變異數下顯著水準接近 0.05， 但若誤差項具異質變異數下， 則顯著水準會比設定的 0.05 高上許多。 因此在不確定變異數是否具同質變異數下， 使用 HC 標準誤是較保守也正確的選擇。