【推薦書籍】
統計學(含概要)歷屆試題詳解、
統計學:重點觀念與題解(上) 、統計學:重點觀念與題解(下) 、計量經濟學與財務工程、
統計學精選666題
【推薦課程】
行動版、數位課程
篇名
辛普森悖論
作者
許誠哲
說明
發佈時間:20260202
Simpson’s paradox (辛普森悖論)是統計中一種特殊現象,表示若將資料分成幾個群體各別分析與將群體混合分析會有完全相反的結論。20 世紀初就有許多人討論此一現象, 但英國密碼破譯員 Edward Hugh Simpson (1922-2019) 在 1951 年首次以正式文獻探討。以條件機率的方式説明, 即為給定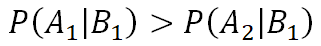 且
且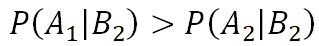 ,但卻出現
,但卻出現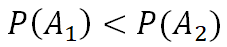 。舉例來說,以下是兩球員在 1995、1996 年的打擊表現(安打/打數 = 打擊率):
。舉例來說,以下是兩球員在 1995、1996 年的打擊表現(安打/打數 = 打擊率):
| 球季 | Derek Jeter | David Justice |
|---|---|---|
| 1995 | 12/48 = 0.250 | 104/411 = 0.253 |
| 1996 | 183/582 = 0.314 | 45/140 = 0.321 |
| 總和 | 195/630 = 0.310 | 149/551 = 0.270 |
可以看出單年來看,David Justice 的打擊率都高於 Derek Jeter,但如果兩年合併,Derek Jeter 的打擊率反而較高。造成此現象的原因是 David Justice 打擊率較低的那一年打數較多,打擊率較高的那一年的打數較少,因此合併後的打擊率會較低。歷史上最著名的例子是 UC Berkeley 的錄取範例(錄取人數/申請人數 = 錄取率)。
| 學院 | 男性 | 女性 |
|---|---|---|
| A | 512/825 = 62% | 89/108 = 82% |
| D | 138/417 = 33% | 131/375 = 35% |
| 總和 | 650/1242 = 52% | 220/483 = 46% |
可以看出 A, D 學院中,女性錄取率都高於男性,但如果合併看,男性錄取率反而較高。造成此現象的原因是錄取率較高的學院 A 男性的申請人數較多,因此合併後的錄取率會較高。造成 Simpson’s paradox 的主要原因有二
- 分組樣本數不平衡: 如上面兩個範例所示
- 存在遺漏變數 (omitted variable): 例如年齡較高則所得通常較高,但實際上 30-40 歲的平均所得會高於 50-60 歲的平均所得,主要原因是 30-40 歲的平均教育程度較高,因此教育程度為遺漏變數。
關鍵詞
辛普森悖論、Simpson’s paradox
刊名
商研所許誠哲
該期刊-上一篇
該期刊-下一篇

